
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海举办,本届展会共有来自172个国家、地区和国际组织参会,3600多家企业参展,超过40万名采购商到会洽谈采购,其中中国馆更是吸引众人眼球.为了使博览会有序进行,组委会安排6名志愿者到中国馆的某4个展区提供服务,要求![]() 展区各安排一名志愿者,其余两个展区各安排两名志愿者,其中小马和小王不在一起,则不同的安排方案共有( )
展区各安排一名志愿者,其余两个展区各安排两名志愿者,其中小马和小王不在一起,则不同的安排方案共有( )
A.156种B.168种C.172种D.180种
科目:高中数学 来源: 题型:
【题目】设函数![]() x∈R,其中a,b∈R.
x∈R,其中a,b∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0,且f(x1)= f(x0),其中x1≠x0,求证:x1+2x0=3;
(Ⅲ)设a>0,函数g(x)= |f(x)|,求证:g(x)在区间[0,2]上的最大值不小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在进入“互联网+”时代,大学生小张自己开了一家玩具店,他通过“互联网+”销售某种玩具,经过一段时间对一种玩具的销售情况进行统计,得5数据如下:
假定玩具的销售量![]() (百个)与玩具的销售价价格
(百个)与玩具的销售价价格![]() (元)之间存在相关关系:
(元)之间存在相关关系:
销售量 | 2 | 3 | 4 | 5 | 6 | 8 |
单个玩具的销售价 | 5.5 | 4.3 | 3.9 | 3.8 | 3.7 | 3.6 |
根据以上数据,小张分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)以![]() 为解释变量,
为解释变量,![]() 为预报变量,作出散点图;
为预报变量,作出散点图;
(2)分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
,![]() 大小,判断哪个模型拟后效果更好.
大小,判断哪个模型拟后效果更好.
(3)若—个玩具进价0.5元,依据(2)中拟合效果好的模型判断该玩具店有无亏损的可能?
查看答案和解析>>
科目:高中数学 来源: 题型:
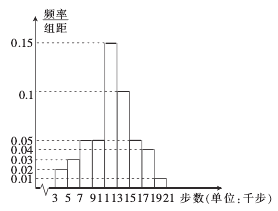
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
分组 (单位:千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有![]() %的把握认为是否为“健步达人”与年龄有关;
%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)(ⅰ)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(ⅱ)由频率分布直方图可以认为,不超过40岁的市民日健步步数![]() (单位:千步)近似地服从正态分布
(单位:千步)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 的值已求出约为
的值已求出约为![]() .现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数
.现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数![]() 位于
位于![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
参考公式: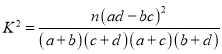 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
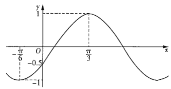
【题目】如图是函数![]() 的部分图象,把函数
的部分图象,把函数![]() 的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象向左平移
的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A.函数![]() 是偶函数
是偶函数
B.函数![]() 图象的对称轴为直线
图象的对称轴为直线![]()
C.函数![]() 的单调递增区间为
的单调递增区间为![]()
D.函数![]() 图象的对称中心为
图象的对称中心为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(简称:AQI)是定量描述空气质量状况的无量纲指数,空气质量按照AQI大小分为六级:![]() 为优,
为优,![]() 为良,
为良,![]() 为轻度污染,
为轻度污染,![]() 为中度污染,
为中度污染,![]() 为重度污染,
为重度污染,![]() 为严重污染.下面记录了北京市
为严重污染.下面记录了北京市![]() 天的空气质量指数,根据图表,下列结论错误的是( )
天的空气质量指数,根据图表,下列结论错误的是( )
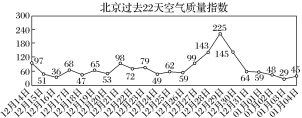
A.在北京这![]() 天的空气质量中,按平均数来考查,最后
天的空气质量中,按平均数来考查,最后![]() 天的空气质量优于最前面
天的空气质量优于最前面![]() 天的空气质量
天的空气质量
B.在北京这![]() 天的空气质量中,有
天的空气质量中,有![]() 天达到污染程度
天达到污染程度
C.在北京这![]() 天的空气质量中,
天的空气质量中,![]() 月
月![]() 日空气质量最差
日空气质量最差
D.在北京这![]() 天的空气质量中,达到空气质量优的天数有
天的空气质量中,达到空气质量优的天数有![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三峡大坝专用公路沿途山色秀美,风景怡人.为确保安全,全程限速为80公里/小时.为了解汽车实际通行情况,经过监测发现某时段200辆汽车通过这段公路的车速均在[50,90](公里/小时)内,根据监测结果得到如下组距为10的频率分布折线图:
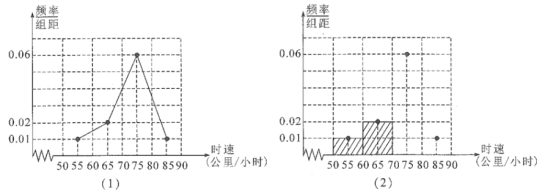
(1)请根据频率分布折线图,将颊率分布直方图补充完整(用阴影部分表示);
(2)求这200辆汽车在该路段超速的车辆数以及在该路段的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com