Question

【题目】函数f（x）=cos x，对任意的实数t，记f（x）在[t，t+1]上的最大值为M（t），最小值为m（t），则函数h（t）=M（t）﹣m（t）的值域为 ．

Answer 1

【答案】
【解析】解：解：函数f（x）=cos x的周期为T= =4，1）当4n﹣1≤t≤4n，n∈Z，区间[t，t+1]为增区间，则有m（t）=cos ，M（t）=cos =sin ，
2）当4n＜t＜4n+1，n∈Z，①若4n＜t≤4n+ ，
则M（t）=1，m（t）=sin ，
②若4n+ ＜t＜4n+1，则M（t）=1，m（t）=sin ，
3）当4n+1≤t≤4n+2，则区间[t，t+1]为减区间，则有M（t）=cos ，m（t）=sin ；
4）当4n+2＜t＜4n+3，则m（t）=﹣1，
①当4n+2＜t≤4n+ 时，M（t）=cos ，
②当4n+ ＜t＜4n+3时，M（t）=sin ；则有h（t）=M（t）﹣m（t）
=
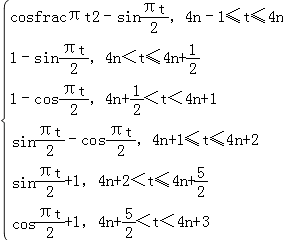
当4n﹣1≤t≤4n，h（t）的值域为[1， ]，
当4n＜t≤4n+ ，h（t）的值域为[1﹣ ，1），
当4n+ ＜t＜4n+1，h（t）的值域为（1﹣ ，1），
当4n+1≤t≤4n+2，h（t）的值域为[1， ]，
当4n+2＜t≤4n+ 时，h（t）的值域为[1﹣ ，1），
当4n+ ＜t＜4n+3时，h（t）的值域为[1﹣ ，1）．
综上，h（t）=M（t）﹣m（t）的值域为 ．
故答案是： ．