
已知半径为 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
(1)V=4
 ;(2)V=8;(3)球的表面积与其内接正方体的全面积之比为
;(2)V=8;(3)球的表面积与其内接正方体的全面积之比为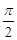 .
.
解析试题分析:(1)球的体积公式为V=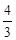
 R3,将R=
R3,将R= 代入可得V=4
代入可得V=4
 ;(2)要求内接正方体的体积,需要知道正方体的棱长,正方体的对角线是球的直径,而正方体的对角线是棱长的
;(2)要求内接正方体的体积,需要知道正方体的棱长,正方体的对角线是球的直径,而正方体的对角线是棱长的 倍,设正方体的棱长为a,所以2
倍,设正方体的棱长为a,所以2 =
= a,a="2," V=a3=8;(3)求出正方体的表面积和球的表面积,从而得出球的球面面积与其内接正方体的全面积之比,S球=4
a,a="2," V=a3=8;(3)求出正方体的表面积和球的表面积,从而得出球的球面面积与其内接正方体的全面积之比,S球=4 R2=12
R2=12 ,S正方体=6a2=24,所以这个球的表面积与其内接正方体的全面积之比为12
,S正方体=6a2=24,所以这个球的表面积与其内接正方体的全面积之比为12 :24=
:24=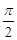 .
.
试题解析:(1)球的体积V=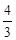
 R3=4
R3=4
 ;
;
(2)设正方体的棱长为a,
∴2 =
=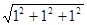 a =
a = a,a="2," V=a3=8;
a,a="2," V=a3=8;
(3)S球=4 R2=12
R2=12 ,
,
S正方体=6a2=24,
∴这个球的表面积与其内接正方体的全面积之比为12 :24=
:24=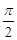 .
.
考点:1.球的体积公式;2.球内接多面体.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
某工厂为了制造一个实心工件,先画出了这个工件的三视图(如图),其中正视图与侧视图为两个全等的等腰三角形,俯视图为一个圆,三视图尺寸如图所示(单位cm);
(1)求出这个工件的体积;
(2)工件做好后,要给表面喷漆,已知喷漆费用是每平方厘米1元,现要制作10个这样的工件,请计算喷漆总费用(精确到整数部分).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四棱锥 的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.

(1)求证: ;
;
(2)若 为
为 的中点,求直线
的中点,求直线 与平面
与平面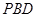 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形,且侧面AA1C1C是边长为2的正方形,E是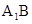 的中点,F在棱CC1上。
的中点,F在棱CC1上。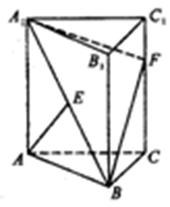
(1)当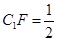 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积;
(2)当点F使得A1F+BF最小时,判断直线AE与A1F是否垂直,并证明的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C丄平面ABCD,且AB=BC=CA=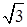 ,AD=CD=1.
,AD=CD=1.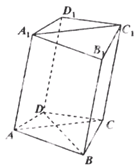
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且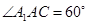 ,求四棱柱
,求四棱柱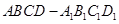 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com