
(
东北师大附中模拟)如下图,在直角梯形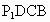 中,
中,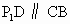 ,
,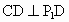 ,
,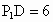 ,BC=3,
,BC=3,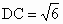 ,A是
,A是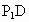 的中点,E是线段AB的中点,沿AB把平面
的中点,E是线段AB的中点,沿AB把平面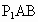 折起到平面PAB的位置,使二面角P—CD—B成45°.
折起到平面PAB的位置,使二面角P—CD—B成45°.
(1)
求证:PA⊥平面ABCD;(2)
求平面PEC和平面PAD所成的锐二面角的大小.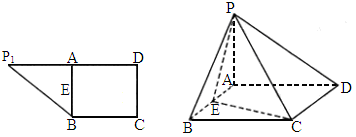
|
解析:证明: (1)∵AB⊥PA,AB⊥AD,∴AB⊥平面PAD.∵ AB∥DC,DC⊥平面PAD.∴ DC⊥PD,DC⊥AD,∴∠PDA为二面角P-CD-B的平面角. (3分)故∠ PDA=45°.∵PA=AD=3,∴∠ APD=45°.∴PA⊥AD.又 PA⊥AB,∴PA⊥平面ABCD. (6分)(2) 证法一:延长DA,CE交于点N,连结PN,由折叠知 PE=NE,又∵E为中点,∴NE=CE.∴ PE=NE=CE,PN⊥PC.又由 (1)知PN⊥PD.∴∠ CPD为二面角C-PN-D的平面角. (9分)在直角三角形 PDC中,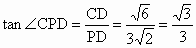 ,∴∠CPD=30°. ,∴∠CPD=30°.
即平面 PEC和平面PAD所成锐二面角为30°. (12分)
证法二:如图建立空间直角坐标系 A-xyz,则 P(0,0,3),D(0,3,0),E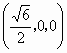 ,C ,C . .
∴ 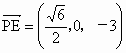 , ,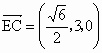 , ,
设 n=(x,y,z)为平面PEC的法向量,则
又平面 PAD的法向量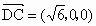 , ,
∴ 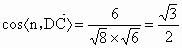 . .
∴ 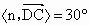 ,即所求二面角为30°. ,即所求二面角为30°. |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:013
(
东北师大附中模拟)设集合M={1,2,3,4,5},选择M的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有[
]|
A .50种 |
B .49种 |
C .48种 |
D .47种 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(
东北师大附中模拟)一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:(1)
连续取两次都是红球的概率;(2)
如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取球次数ξ的概率分布列及期望.查看答案和解析>>
科目:高中数学 来源: 题型:013
(
东北师大附中模拟)平面α∥平面β的一个充分条件是[
]A
.存在一条直线a,a∥α,a∥βB
.存在一条直线a,a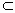 α,a∥β
α,a∥β
C
.存在两条平行直线a,b,a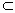 α,b
α,b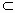 β,a∥β,b∥α
β,a∥β,b∥α
D
.存在两条异面直线a,b,a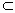 α,b
α,b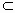 β,a∥β,b∥α
β,a∥β,b∥α查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com