练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知命题p：在区间上存在单调递减区间；命题q：函数，且有三个实根.若为真命题，则实数的取值范围是：（ ）

    A.B.C.D.

    【答案】C

    【解析】

    根据命题p：在区间上存在单调递减区间，

    转化为命题：在区间上不存在单调递减区间，即在区间上恒成立求解.根据有三个实根，转化为有三个实根求解，为真命题，则两者取交集.

    因为命题p：在区间上存在单调递减区间，

    所以命题：在区间上不存在单调递减区间，

    所以在区间上恒成立，

    即在区间上恒成立，

    因为在区间上是减函数，

    所以，

    所以.

    所以命题：.

    因为，

    所以，

    又因为有三个实根，

    所以有三个实根，

    即有三个实根，

    令，

    ，

    当或时，，t是增函数，

    当时，，t是减函数，

    所以当时，t取得最大值，

    当时，t取得最小值，

    所以.

    若为真命题，则实数的取值范围是：.

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某学校共有名学生，其中男生人，为了解该校学生在学校的月消费情况，采取分层抽样随机抽取了名学生进行调查，月消费金额分布在之间．根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示：

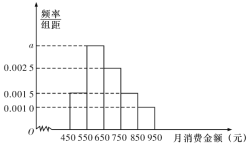
    将月消费金额不低于元的学生称为“高消费群”．

    （1）求的值，并估计该校学生月消费金额的平均数（同一组中的数据用该组区间的中点值作代表）；

    （2）现采用分层抽样的方式从月消费金额落在，内的两组学生中抽取人，再从这人中随机抽取人，记被抽取的名学生中属于“高消费群”的学生人数为随机变量，求的分布列及数学期望；

    （3）若样本中属于“高消费群”的女生有人，完成下列列联表，并判断是否有的把握认为该校学生属于“高消费群”与“性别”有关？

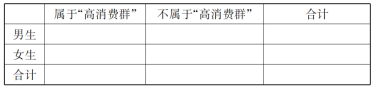
    （参考公式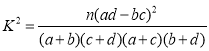：，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且椭圆C过点．

    (1)求椭圆C的标准方程；

    (2)过椭圆C的右焦点的直线l与椭圆C交于A、B两点，且与圆：交于E、F两点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆：的离心率为，过左焦点且斜率为的直线交椭圆于两点，线段的中点为，直线：交椭圆于两点.

    （1）求椭圆的方程；

    （2）求证：点在直线上；

    （3）是否存在实数，使得？若存在，求出的值，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额（万元）的数据如下：

    加盟店个数（个）

    1

    2

    3

    4

    5

    单店日平均营业额（万元）

    10.9

    10.2

    9

    7.8

    7.1

    （1）求单店日平均营业额（万元）与所在地区加盟店个数（个）的线性回归方程；

    （2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数的所有可能取值；

    （3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.

    （参考数据及公式：，，线性回归方程，其中，.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列与满足：，且为正项等比数列，，.

    （1）求数列与的通项公式；

    （2）若数列满足，为数列的前项和，证明：.

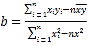    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在xOy中，曲线的参数方程为（t为参数）.在以坐标原点O为极点，x轴正半轴为极轴的极坐标系中，曲线：，曲线：，.

    （1）把的参数方程化为极坐标方程；

    （2）设分别交，于点P，Q，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（单位：分.百分制，均为整数）分成，，，，，六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题.

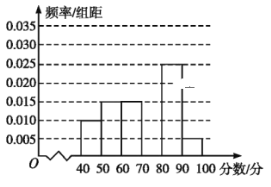
    （1）求分数在内的频率，并补全这个频率分布直方图；

    （2）从频率分布直方图中，估计本次考试成绩的众数和平均数；

    （3）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    (1)当时，讨论函数的单调性

    (2)当时，，对任意，都有恒成立，求实数b的取值范围.

    查看答案和解析>>

    同步练习册答案