
【题目】已知数列{an}满足:an+1+(﹣1)nan=n+2(n∈N*),则S20=( )
A.130
B.135
C.260
D.270
【答案】A
【解析】解:∵an+1+(﹣1)nan=n+2,
∴a2﹣a1=3,a3+a2=4,a4﹣a3=5.
可得a3+a1=1,a2+a4=9,
同理可得:a5+a7=a3+a1=1=a9+a11=a13+a15=a17+a19.
a6+a8=17,a10+a12=25,a14+a16=33,a18+a20=41.
∴{an}的前20项和=(a1+a3)+…+(a17+a19)+(a2+a4)+(a6+a8)+…+(a18+a20)
=5+9+17+25+33+41=130.
故选:A.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF= ![]() AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( ) 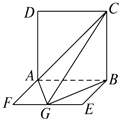
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且满足 ![]() +
+ ![]() =4cosC. (Ⅰ)求
=4cosC. (Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)若tanA=2tanB,求sinA的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上. 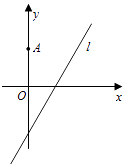
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年12月1日,汉孝城际铁路正式通车运营.除始发站(汉口站)与终到站(孝感东站)外,目前沿途设有7个停靠站,其中,武汉市辖区内有4站(后湖站、金银潭站、天河机场站、天河街站),孝感市辖区内有3站(闵集站、毛陈站、槐荫站).为了了解该线路运营状况,交通管理部门计划从这7个车站中任选3站调研.
(1)求孝感市辖区内至少选中1个车站的概率;
(2)若孝感市辖区内共选中了X个车站,求随机变量X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题: ①共线向量是在同一条直线上的向量;
②若两个向量不相等,则它们的终点不可能是同一点;
③与已知非零向量共线的单位向量是唯一的;
④若四边形ABCD是平行四边形,则 ![]() 与
与 ![]() ,
, ![]() 与
与 ![]() 分别共线.
分别共线.
其中正确命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,且其图象向左平移
)的最小正周期为π,且其图象向左平移 ![]() 个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com