
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.函数
轴平行.函数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:函数![]() 共有两个零点,一个零点是
共有两个零点,一个零点是![]() ,另一个零点
,另一个零点![]() 在区间
在区间![]() 内;
内;
(Ⅲ)求证:存在![]() ,当
,当![]() 时,
时, ![]() .
.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
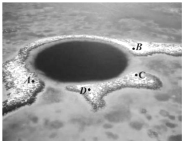
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某营养协会对全市18岁男生的身高作调查,统计显示全市18岁男生的身高服从正态分布![]() ,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于
,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于![]() 到
到![]() 之间.现将结果按如下方式分为6组,第一组
之间.现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
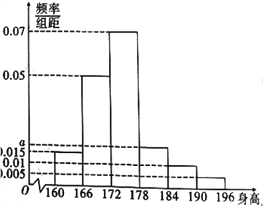
(1)若全市18岁男生共有![]() 人,试估计该市身高在
人,试估计该市身高在![]() 以上的18岁男生人数;
以上的18岁男生人数;
(2)求![]() 的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
(3)若身高![]() 以上的学生校服需要单独定制,现从这100名学生中身高在
以上的学生校服需要单独定制,现从这100名学生中身高在![]() 以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为
以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附: ![]() ,则
,则![]() ;
;
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,
中点,![]() .
.

(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x+1)2+(y-3)2=9和圆C2:x2+y2-4x+2y-11=0.
(1)求两圆公共弦所在直线的方程;
(2)求直线过点C(3,-5),且与公共弦垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为[0,1]的函数f(x)同时满足以下三个条件:
①对任意的x∈[0,1],总有f(x)≥0;
②f(1)=1;
③当x1,x2∈[0,1],且x1+x2∈[0,1]时,f(x1+x2)≥f(x1)+f(x2)成立.称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知f(x)为“友谊函数”,求f(0)的值;
(2)函数g(x)=2x-1在区间[0,1]上是否为“友谊函数”?请给出理由;
(3)已知f(x)为“友谊函数”,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,求证: f(x0)=x0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
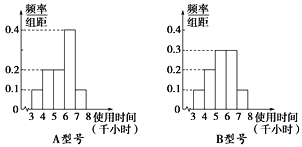
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的极坐标方程为:ρ2-4![]() ρcos(θ-
ρcos(θ-![]() )+6=0.
)+6=0.
(1)将极坐标方程化为普通方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com