
分析 (Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;
(Ⅱ)根据(Ⅰ)通过讨论a的范围,确定出满足条件的a的范围即可.
解答 解:(Ⅰ)f(x)=lnx-a(x-1)2-(x-1),(x>0),
f′(x)=-$\frac{(2ax+1)(x-1)}{x}$,
①a<-$\frac{1}{2}$时,0<-$\frac{1}{2a}$<1,
令f′(x)<0,解得:x>1或0<x<-$\frac{1}{2a}$,令f′(x)>0,解得:-$\frac{1}{2a}$<x<1,
∴f(x)在$(0,-\frac{1}{2a}),(1,+∞)$递减,在$(-\frac{1}{2a},1)$递增;
②-$\frac{1}{2}$<a<0时,令f′(x)<0,解得:x>-$\frac{1}{2a}$或0<x<1,令f′(x)>0,解得:1<x<-$\frac{1}{2a}$,
∴f(x)在$(0,1),(-\frac{1}{2a},+∞)$递减,在$(1,-\frac{1}{2a})$递增;
③$a=-\frac{1}{2}$,f′(x)=-$\frac{{(x-1)}^{2}}{x}$≤0,f(x)在(0,1),(1+∞)递减;
④a≥0时,2ax+1>0,令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(Ⅱ)函数恒过(1,0),由(Ⅰ)得:a≥-$\frac{1}{2}$时,符合题意,
a<-$\frac{1}{2}$时,
f(x)在(0,-$\frac{1}{2a}$)递减,在$(-\frac{1}{2a},1)$递增,不合题意,
故a≥-$\frac{1}{2}$.
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{2016}{2017}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{4030}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点O在圆外 | B. | 点O在圆上 | C. | 点O在圆内 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
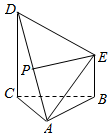 如图,在四棱锥A-BCDE中,侧面ABC为正三角形,DC=BC=2BE,BE∥CD,DC⊥BC,且侧面ABC⊥底面BCDE,P为AD的中点.
如图,在四棱锥A-BCDE中,侧面ABC为正三角形,DC=BC=2BE,BE∥CD,DC⊥BC,且侧面ABC⊥底面BCDE,P为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
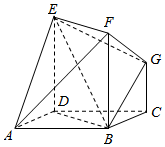 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE,CG=$\frac{1}{2}$DE.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE,CG=$\frac{1}{2}$DE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
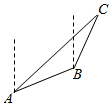 一艘海轮从A出发,沿北偏东75°的方向航行(2$\sqrt{3}$-2)nmile到达海岛B,然后从B出发,沿北偏东15°的方向航行4nmile到达海岛C.
一艘海轮从A出发,沿北偏东75°的方向航行(2$\sqrt{3}$-2)nmile到达海岛B,然后从B出发,沿北偏东15°的方向航行4nmile到达海岛C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com