
已知函数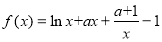 .
.
(1)当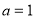 时,求曲线
时,求曲线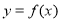 在点
在点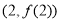 处的切线方程;
处的切线方程;
(2)当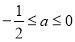 时,讨论
时,讨论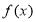 的单调性.
的单调性.
(1)
(2)当 时,在
时,在 ,
, 单调递减,在
单调递减,在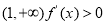 ,
, 单调递增;
单调递增;
当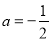 时,在
时,在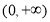 单调递减
单调递减
当 时,在
时,在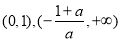
 单调递减,
单调递减, 在
在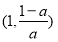 单调递增;
单调递增;
【解析】
试题分析:(1)利用切点处的导函数值是切线的斜率,应用直线方程的点斜式即得;
(2)求导数 ,
,
根据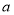 的不同取值情况,研究导数值的正负,确定函数的单调性.
的不同取值情况,研究导数值的正负,确定函数的单调性.
本题易错,分类讨论不全或重复.
试题解析:(1)当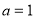 时,
时,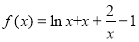 ,
,
此时 , 2分
, 2分
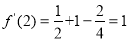 ,又
,又 ,
,
所以切线方程为: ,
,
整理得: ;
;  分
分
(2) , 6分
, 6分
当 时,
时, ,此时,在
,此时,在 ,
, 单调递减,
单调递减,
在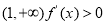 ,
, 单调递增; 8分
单调递增; 8分
当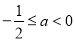 时,
时, ,
,
当 即
即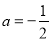 时
时 在
在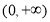 恒成立,
恒成立,
所以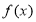 在
在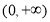 单调递减; 10分
单调递减; 10分
当 时,
时, ,此时在
,此时在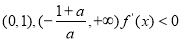 ,
, 单调递减,
单调递减, 在
在 单调递增; 12分
单调递增; 12分
综上所述:当 时,
时, 在
在 单调递减,
单调递减, 在
在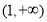 单调递增;
单调递增;
当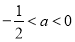 时,
时,  在
在 单调递减,
单调递减, 在
在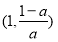 单调递增;
单调递增;
当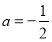 时
时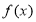 在
在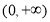 单调递减. 13分
单调递减. 13分
考点:应用导数研究函数的单调性,导数的几何意义,直线方程的点斜式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试理科数学试卷(解析版) 题型:选择题
将函数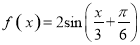 的图象向左平移
的图象向左平移 个单位,再向下平移1个单位,得到函数 g( x)的图象,则 g( x)的解析式为( )
个单位,再向下平移1个单位,得到函数 g( x)的图象,则 g( x)的解析式为( )
A. B.
B.
C.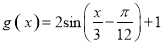 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试理科数学试卷(解析版) 题型:选择题
设函数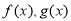 满足下列条件:
满足下列条件:
(1)对任意实数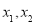 都有
都有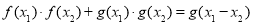 ;
;
(2)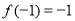 ,
,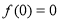 ,
,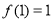 .
.
下列四个命题:
①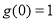 ;
;
② ;
;
③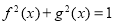 ;
;
④当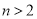 ,
,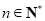 时,
时,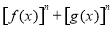 的最大值为
的最大值为 .
.
其中所有正确命题的序号是( )
A.①③ B.②④ C.②③④ D.①③④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试文科数学试卷(解析版) 题型:解答题
已知数列 的前
的前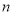 项和为
项和为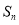 ,且
,且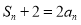 ,数列
,数列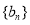 满足
满足 ,且
,且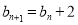 .
.
(1)求数列 ,
,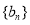 的通项公式;
的通项公式;
(2)设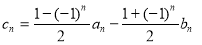 ,求数列
,求数列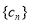 的前
的前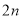 项和
项和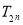 .
.
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知数列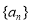 是等差数列,且
是等差数列,且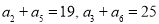 .
.
(Ⅰ)求数列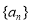 的通项公式;
的通项公式;
(Ⅱ)若数列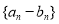 是首项为2,公比为2的等比数列,求数列
是首项为2,公比为2的等比数列,求数列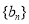 的前
的前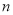 项和
项和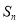 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试文科数学试卷(解析版) 题型:填空题
已知抛物线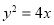 的准线与双曲线
的准线与双曲线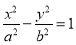 的两条渐近线分别交于
的两条渐近线分别交于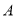 ,
,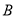 两点,且
两点,且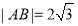 ,则双曲线的离心率
,则双曲线的离心率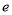 为 .
为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一文科数学试卷(解析版) 题型:解答题
某数学兴趣小组有男女生各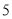 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
.
(1)求 ,
, 的值;
的值;
(2)现从成绩高于 分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com