
【题目】已知立方和公式:![]()
![]() 求函数
求函数![]() 的值域;
的值域;
![]() 求函数
求函数![]() ,
,![]() 的值域;
的值域;
![]() 若任意实数x,不等式
若任意实数x,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先化简f(x)![]() sin(x
sin(x![]() ),再根据三角函数的性质即可求出,
),再根据三角函数的性质即可求出,
(2)化简g(x)![]() ,再设sinx+cosx=t
,再设sinx+cosx=t![]() sin(x
sin(x![]() ),可得t∈[1,
),可得t∈[1,![]() ],可得g(x)=h(t)
],可得g(x)=h(t)![]() (
(![]() t),根据函数的单调性即可求出,
t),根据函数的单调性即可求出,
(3)化简sin6x+cos6x=1﹣3sin2xcos2x,设sinxcosx=t,即t![]() sin2x,则
sin2x,则![]() t
t![]() ,则原不等式转化为3t2﹣at﹣1≤0在t∈[
,则原不等式转化为3t2﹣at﹣1≤0在t∈[![]() ,
,![]() ]恒成立,即可求出a的范围
]恒成立,即可求出a的范围
解:![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
故函数![]() 的值域为
的值域为![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
易知函数![]() 在
在![]() 上为减函数,
上为减函数,![]() ,
,![]() ,
,
![]() 函数
函数![]() 的值域为
的值域为![]() .
.
![]() ,
,
![]() ,
,
设![]() ,即
,即![]() ,则
,则![]() ,
,
![]() 不等式
不等式![]() 恒成立,
恒成立,
![]() ,在
,在![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,
恒成立,
 ,
,
解得![]() ,
,
故a的取值范围为![]()


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】将编号![]() 的小球放入编号为
的小球放入编号为![]() 的盒子中,要求不允许有空盒子,且球与盒子的号不能相同,则不同的放球方法有( )
的盒子中,要求不允许有空盒子,且球与盒子的号不能相同,则不同的放球方法有( )
A. 16种 B. 12种 C. 9种 D. 6种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() .
.
(Ⅰ)求函数![]() 在R上的解析式;
在R上的解析式;
(Ⅱ)若![]() ,函数
,函数![]() ,是否存在实数m使得
,是否存在实数m使得![]() 的最小值为
的最小值为![]() ,若存在,求m的值;若不存在,请说明理由.
,若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有下列结论:
,有下列结论:
①![]() 的定义域为(-1, 1); ②
的定义域为(-1, 1); ②![]() 的值域为(
的值域为(![]() ,
, ![]() );
);
③![]() 的图象关于原点成中心对称; ④
的图象关于原点成中心对称; ④![]() 在其定义域上是减函数;
在其定义域上是减函数;
⑤对![]() 的定义城中任意
的定义城中任意![]() 都有
都有![]() .
.
其中正确的结论序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1=2,an+1=3an+2n﹣1.
(1)求证:数列{an+n}为等比数列;
(2)记bn=an+(1﹣λ)n,且数列{bn}的前n项和为Tn , 若T3为数列{Tn}中的最小项,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
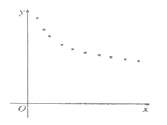
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为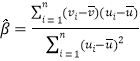 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为![]() ,
,![]() ,
,![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响
(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com