练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知集合.

    (1)若,问是否存在使;

    (2)对于任意的,是否一定有?并证明你的结论.

    【答案】(1) 一定存在,使成立(2) 不一定有

    【解析】试题分析：（1）根据已知条件知：若a∈A，b∈B，则一定存在n1，n2∈z，使得a=3n1+1，b=3n2+1，所以a+b=3（n1+n2）+3．而集合M的元素需满足：x=6n+3=32n+3，显然n1+n2=2n时成立，（2）根据（1）判断：若n1+n2为奇数，则结论不正确所以不一定有a+b=m且m∈M．

    试题解析：

    (1)令,则.

    再令,则.

    故若,一定存在,使成立.

    (2)不一定有.

    证明如下:设,

    则.

    因为所以.

    若为偶数,令,

    则,此时.

    若为奇数,令,

    则,此时

    综上可知,对于任意的不一定有.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知空间四边形ABCD，E、H分别是AB、AD的中点，F、G分别是边BC、DC的三等分点（如图），
    求证：
    （1）对角线AC、BD是异面直线；
    （2）直线EF和HG必交于一点，且交点在AC上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示

    年份200x（年）

    0

    1

    2

    3

    4

    人口数y（十）万

    5

    7

    8

    11

    19


    （1）请画出上表数据的散点图；
    （2）请根据上表提供的数据，求出Y关于x的线性回归方程Y=bx+a；
    （3）据此估计2005年该城市人口总数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= sin2x+cos2x．
    （1）当x∈[0， ]时，求f（x）的取值范围；
    （2）求函数y=f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设F1 ， F2分别是椭圆 =1的左、右焦点．
    （1）若M是该椭圆上的一点，且∠F1MF2=120°，求△F1MF2的面积；
    （2）若P是该椭圆上的一个动点，求 的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）讨论的单调性；

    （2）若，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的一个焦点与抛物线y2=8x的焦点重合，点 在C上．
    （1）求椭圆C的方程；
    （2）若椭圆C的一条弦被M（2，1）点平分，求这条弦所在的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.

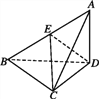
    (1)求证:平面ABC⊥平面ACD;

    (2)若E为AB中点,求点A到平面CED的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设{an}为等差数列，Sn是其前n项和，已知S7=7，S15=75，Tn为数列{ }的前n项和，
    （1）求a1和d；
    （2）求Tn ．

    查看答案和解析>>

    同步练习册答案