
【题目】某网红直播平台为确定下一季度的广告投入计划,收集了近6个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
广告投入量/万元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/万元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
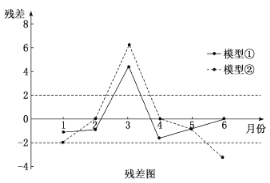
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由.
(2)残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除的异常数据是哪一组?
(ii)剔除异常数据后,求出(1)中所选模型的回归方程;
(iii)广告投入量![]() 时,(ii)中所得模型收益的预报值是多少?
时,(ii)中所得模型收益的预报值是多少?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: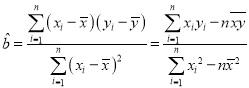 ,
,![]() .
.
【答案】(1)模型①,理由见解析;(2)(i)是3月份的数据; (ii)![]() ; (iii)62.04万元.
; (iii)62.04万元.
【解析】
(1)根据残差图中体现出的残差点分布,结合其均匀程度以及带状区域的宽窄,即可分析比较;
(2)(i)根据题意,结合残差图,即可求得![]() 月份的数据异常,应该剔除;
月份的数据异常,应该剔除;
(ii)根据已知数据和![]() 月份的数据,结合
月份的数据,结合![]() 和
和![]() 的计算公式,即可求得结果;
的计算公式,即可求得结果;
(iii)令![]() ,代入(ii)中所求回归直线方程,即可求得结果.
,代入(ii)中所求回归直线方程,即可求得结果.
(1)应该选择模型①,因为模型①的残差点比较均匀地落在水平的带状区域中,
且模型①的带状区域比模型②的带状区域窄,
所以模型①的拟合精度高,回归方程的预报精度高.
(2)(i)剔除异常数据是3月份的数据,即![]() ;
;
(ii)剔除异常数据,即3月份的数据后,得
![]() ,
,
![]()
![]() ,
,
![]() .
.
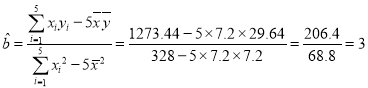 ,
,![]() .
.
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(iii)把![]() 代入(i)中所求回归方程得
代入(i)中所求回归方程得
![]() ,
,
故预报值为62.04万元.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用50元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 是边长为4的正方形,平面
是边长为4的正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求二面角![]() 的余弦值;
的余弦值;
(2)在线段![]() 是否存在点
是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设自然数![]() 。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当
。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当![]() 时,排列
时,排列![]() 就满足要求)。
就满足要求)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,设离心率为
,设离心率为![]() ,且满足
,且满足![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点(0,1)的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: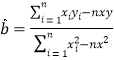 ,
,![]() (精确到
(精确到![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com