
 (含80)以上时,属醉酒驾车.”
(含80)以上时,属醉酒驾车.” 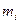 与
与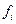 分别表示图 图乙
分别表示图 图乙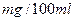 (含70)以上,但他俩坚称没喝那么多,是测试仪不准,交警大队陈队长决定在被酒精测试仪测得酒精浓度在70
(含70)以上,但他俩坚称没喝那么多,是测试仪不准,交警大队陈队长决定在被酒精测试仪测得酒精浓度在70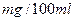 (含70)以上的酒后驾车者中随机抽出2人抽血检验,求吴、李两位先生至少有1人被抽中的概率.
(含70)以上的酒后驾车者中随机抽出2人抽血检验,求吴、李两位先生至少有1人被抽中的概率.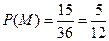
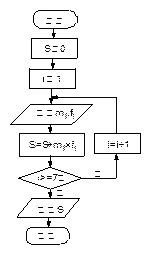
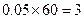 (人)
(人)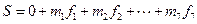
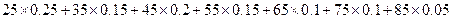 =47(mg/100ml)
=47(mg/100ml)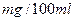 (含70)以上人数为:
(含70)以上人数为: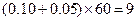
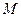 表示吴、李两位先生至少有1人被抽中这一事件,则
表示吴、李两位先生至少有1人被抽中这一事件,则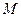 所含的基本事件数为15,
所含的基本事件数为15,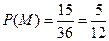 .
. 

 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:不详 题型:解答题
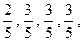 且它们相互独立互不影响。
且它们相互独立互不影响。 表示能成功预约场馆的个数,求随机变量
表示能成功预约场馆的个数,求随机变量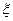 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
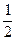 ,乙投篮命中的概率为
,乙投篮命中的概率为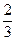 .
. 2个的概率;
2个的概率;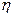 的概率分布和数学期望.
的概率分布和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
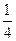 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为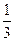

 。
。  表作中至多有两件作品入选“中国馆·贵宾厅”的概率.
表作中至多有两件作品入选“中国馆·贵宾厅”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 跳格游戏:如右图,人从格外只能进入第1格,在格中每次可向前跳1格或2格,那么人从格外跳到第8格的方法种数为( )
跳格游戏:如右图,人从格外只能进入第1格,在格中每次可向前跳1格或2格,那么人从格外跳到第8格的方法种数为( )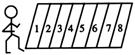
| A.8种 | B.13种 |
| C.21种 | D.34种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
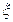 ~
~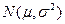 ,且
,且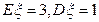 ,那么
,那么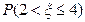 等于( )
等于( )| A.0.5 | B.0.683 | C.0.954 | D.0.997 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com