
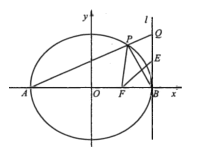
【题目】在平面直角坐标系xOy中,己知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
【答案】(1)![]() (2)
(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)根据椭圆的方程,结合椭圆离心率的求法,即可求出结果;
(2)先由题意,得到直线AP的方程为![]() 代入椭圆方程,求出点P的坐标,表示出
代入椭圆方程,求出点P的坐标,表示出![]() 与
与![]() ,进而可得出结果;
,进而可得出结果;
(3)由直线AP的方程与直线l的方程联立,求出![]() ,表示出直线EF的斜率,再由
,表示出直线EF的斜率,再由![]() 结合韦达定理,以及题中条件,表示出直线PF的斜率,再由题意,即可证明结论成立.
结合韦达定理,以及题中条件,表示出直线PF的斜率,再由题意,即可证明结论成立.
(1)因为椭圆C:![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,
,
所以椭圆C的离心率![]() .
.
(2)因为直线AP的斜率为![]() ,且过椭圆C的左顶点
,且过椭圆C的左顶点![]() ,
,
所以直线AP的方程为![]() .
.
代入椭圆C的方程![]() ,
,
得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
将![]() 代入
代入![]() ,得
,得![]() ,
,
所以点P的坐标为![]() .
.
又椭圆C的右顶点B(2t,0),
所以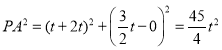 ,
,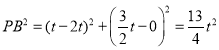 ,
,
所以![]() .
.
(3)直线AP的方程为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,所以
,所以![]() .
.
因为E为线段BQ的中点,所以![]() ,
,
因为焦点F的坐标为(t,0),
所以直线EF的斜率![]() .
.
联立![]() 消y得,
消y得,![]() .
.
由于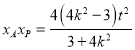 ,
,![]() ,
,
所以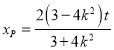 ,
,
所以点P的坐标为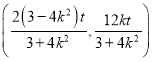 ,
,
所以直线PF的斜率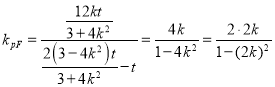 .
.
而直线EF的斜率为2k,
若设![]() ,则有
,则有![]() ,即
,即![]() ,
,
所以点B关于直线EF的对称点在直线PF上.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,沿
,沿![]() 将四边形
将四边形![]() 折起,连接
折起,连接![]() .
.
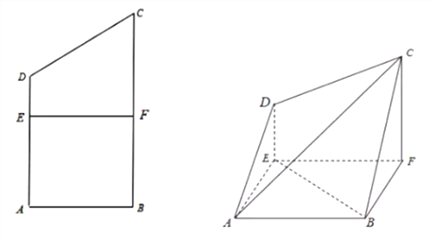
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() .
.
(I)求二面角![]() 的平面角的大小;
的平面角的大小;
(II)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为 2 的正三角形,顶点
是边长为 2 的正三角形,顶点 ![]() 在底面
在底面![]() 上的射影为
上的射影为![]() 的中心,若
的中心,若![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,则三棱锥
,则三棱锥![]() 外接球的表面积为( )
外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家向超市提供的日返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出不超出30件(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利10元. 经统计,试销这10天两个商家每天的销量如图所示的茎叶图(茎为十位数字,叶为个位数字):
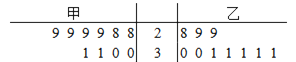
(1)现从甲商家试销的10天中随机抽取两天,求这两天的销售量都小于30件的概率;
(2)根据试销10天的数据,将频率视作概率,用样本估计总体,回答以下问题:
①记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
②超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日返利额的数学期望考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com