
【题目】如图,三棱柱![]() 中,各棱长均相等,
中,各棱长均相等, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
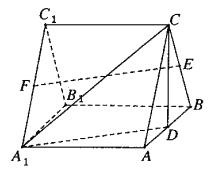
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
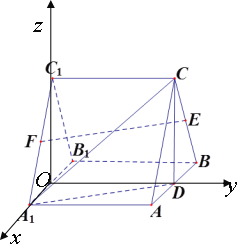
(Ⅱ)若三棱柱![]() 为直棱柱,求直线
为直棱柱,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)详见解析(Ⅱ)详见解析
【解析】【试题分析】(1)依据题设条件,借助运用线面平行的判定定理分析推证;(2)依据题设条件运用线面角的定义构造三角形进行求解或建立空间直角坐标系,运用空间向量的数量积公式探求:
(Ⅰ)证明:在三棱柱![]() 中,
中, ![]() ,且
,且![]() ,
,
连结![]() ,在
,在![]() 中,因为
中,因为![]() ,
, ![]() 分别为棱
分别为棱![]() ,
, ![]() 的中点,所以
的中点,所以![]() ,
, ![]() .
.
又![]() 为
为![]() 的中点,可得
的中点,可得![]() ,所以
,所以![]() ,
, ![]() ,
,
因此四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
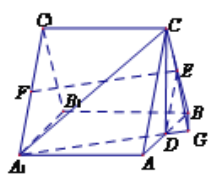
(Ⅱ)证明:由于底面![]() 是正三角形,
是正三角形, ![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
又![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
在平面![]() 内,过点
内,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,连结
,连结![]() ,
,
![]() 平面
平面![]() ,由此得,
,由此得, ![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
设三棱柱的棱长为![]() ,可得
,可得![]() ,由
,由![]() ,所以
,所以![]() ,
,
在![]() 中,
中, ![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2、3、4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(Ⅰ)估计该地区老年人中,需要志愿者提供帮助的老年人比例;
(Ⅱ)能否有![]() 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)中的结论,能否提供更好的调查方法来估计该地区老年人中需要志愿帮助?
附: 
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的图象在点(1,
的图象在点(1, ![]() )处的切线方程;
)处的切线方程;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)已知![]() ,对于函数
,对于函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,其中
,其中![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记
,记![]() ,若
,若![]() 求证
求证![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com