考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用面面垂直的性质定理,得到AC⊥平面CC1B1 B,再由线面垂直的性质得到AC⊥BC1,进一步利用菱形的性质得到B1C⊥BC1,利用线面垂直的判定定理可证;
(2)取AA1的中点,连接DF,EF,分别判断EF,DF与平面平面AB1C平行,得到面面平行,利用面面平行的性质可证.
解答:
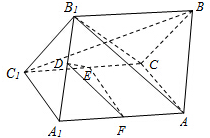
解:(1)∵四边形A A
1 C
1C为矩形,∴AC⊥CC
1,
又平面CC
1B
1 B⊥A A
1 C
1C,CC
1B
1 B∩A A
1 C
1C=CC
1,
∴AC⊥平面CC
1B
1 B,
∵BC
1?平面CC
1B
1 B,
∴AC⊥BC
1,
∵四边形CC
1B
1 B为菱形,∴B
1C⊥BC
1,
又B
1C∩AC=C,AC?平面A
1C,B
1C?平面AB
1C,
∴BC
1⊥平面AB
1C;
(2)取AA
1的中点,连接DF,EF,
∵四边形A A
1 C
1C为矩形,E,F分别是C
1C,AA
1的中点,
∴EF∥AC,又EF?平面平面AB
1C,AC?平面AB
1C,
∴EF∥平面AB
1C,
又D,F分别是A
1 B
1和AA
1的中点,
∴DF∥A B
1,
又DF?平面AB
1C,AB
1?平面AB
1C,
∴DF∥平面AB
1C,
∵EF∩DF=F,EF?平面DEF,DF?平面DEF,
∴平面DEF∥平面AB
1C,
∵DE?平面DEF,
∴DE∥平面AB
1C.
点评:本题考查直线与平面的垂直的判定、直线与平面平行的判定,体现了转化的思想,考查逻辑思维能力 空间想象能力,是中档题.

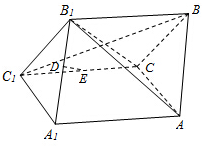 如图,四边形A A1 C1C为矩形,四边形CC1B1 B为菱形,且平面CC1B1 B⊥A A1 C1C,D,E分别是A1 B1和C1C的中点.求证:(1)BC1⊥平面AB1C;
如图,四边形A A1 C1C为矩形,四边形CC1B1 B为菱形,且平面CC1B1 B⊥A A1 C1C,D,E分别是A1 B1和C1C的中点.求证:(1)BC1⊥平面AB1C; 解:(1)∵四边形A A1 C1C为矩形,∴AC⊥CC1,
解:(1)∵四边形A A1 C1C为矩形,∴AC⊥CC1,
