
| A. | -$\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 由题意可得函数在x=0处的切线的斜率为k=f′(0)=2,求得a的值,可得函数的解析式.设函数f(x)的一个极值点为m,由f′(m)=0,可得m的一个值
解答 解:曲线f(x)=cos(2x-$\frac{π}{6}$)+ax在x=0处的切线的斜率为
k=f′(0)=-sin(0-$\frac{π}{6}$)•2+a=1+a,
再根据切线与直线2x-y=0平行,可得1+a=2,
∴a=1,即f(x)=cos(2x-$\frac{π}{6}$)+x.
设函数f(x)的一个极值点为m,
令f′(m)=-sin(2m-$\frac{π}{6}$)•2+1=0,
求得sin(2m-$\frac{π}{6}$)=$\frac{1}{2}$,
故函数f(x)的一个极值点可以是m=$\frac{π}{6}$,
故选:B.
点评 本题主要考查余弦函数的图象,函数在某一点的导数的几何意义,单调性与极值的关系,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:填空题
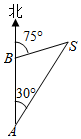 如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.
如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
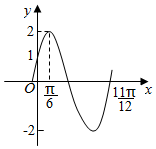 已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.
已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | B. | (-5,1) | ||
| C. | (-5,-1) | D. | (-5,-1)∪(-1,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com