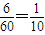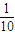已知直线l:x+2y+1=0,集合A={n|n<6,n∈N*},从A中任取3个不同的元素分别作为圆方程(x-a)2+(y-b)2=r2中的a、b、r,则使圆心(a,b)与原点的连线垂直于直线l的概率等于 .
【答案】
分析:本题是一个等可能事件的概率,试验发生包含的事件是从5个元素中任取3个分别作为a、b、r,共有A
53种结果,满足条件的事件是圆心(a,b)与原点的连线垂直于直线l,根据直线垂直的条件写出a,b之间的关系,列举出结果数,得到概率.
解答:解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从5个元素中任取3个分别作为圆方程(x-a)
2+(y-b)
2=r
2中的a、b、r,共有A
53=60种结果,
满足条件的事件是使圆心(a,b)与原点的连线垂直于直线l,即
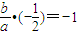
,
∴
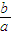
=2,
把一对有序数对分别作为a,b列举出所有结果,(1,2)(2,4)
确定这两个数字以后还有一个r的3种不同取法,共有2×3=6种结果,
∴本题要求的概率是
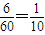
故答案为:
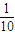 点评:
点评:本题考查等可能事件的概率,考查两条直线垂直的充要条件,考查利用列举与组合数相结合的方法得到事件数,本题是一个综合题目.

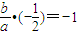 ,
,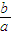 =2,
=2,