
【题目】已知数列{an}满足an+1=a ![]() ﹣nan+1,且a1=2.
﹣nan+1,且a1=2.
(1)计算a2 , a3 , a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明;
(2)求证:2nn≤a ![]() <3nn .
<3nn .
【答案】
(1)解:由已知an+1=a ![]() ﹣nan+1,且a1=2.得到a2=
﹣nan+1,且a1=2.得到a2= ![]() ﹣a1+1=3,a3=
﹣a1+1=3,a3= ![]() ﹣2a2+1=4,a4=
﹣2a2+1=4,a4= ![]() ﹣3a3+1=5;
﹣3a3+1=5;
由此猜测数列{an}的通项公式为an=n+1;
证明:①n=1,2,3,4显然成立;
②假设n=k时成立,即ak=k+1,则n=k+1时,ak+1= ![]() ﹣kak+1=(k+1)2﹣k(k+1)+1=k+2=(k+1)+1;
﹣kak+1=(k+1)2﹣k(k+1)+1=k+2=(k+1)+1;
所以n=k+1时,数列an=n+1也成立;
所以数列{an}的通项公式an=n+1对任意n∈N+都成立
(2)解:因为an=n+1,所以 ![]() =(n+1)n=
=(n+1)n= ![]() >
> ![]() =2nn;
=2nn;
构造函数f(x)=(1+ ![]() )x,则f′(x)=(1+
)x,则f′(x)=(1+ ![]() )xln(1+
)xln(1+ ![]() )(﹣
)(﹣ ![]() )<0,所以函数f(x)为减函数,又x≥1,所以f(x)≤f(1)=2<3,所以
)<0,所以函数f(x)为减函数,又x≥1,所以f(x)≤f(1)=2<3,所以 ![]() =
= ![]() <3,
<3,
即(n+1)n<3nn;
所以2nn≤a ![]() <3nn
<3nn
【解析】(1)由an+1=a ![]() ﹣nan+1,且a1=2,分别令 n=2,3,4即可求解,进而可猜想,然后利用数学归纳法进行证明即可;(2)由(1)可得an=n+1,从而有
﹣nan+1,且a1=2,分别令 n=2,3,4即可求解,进而可猜想,然后利用数学归纳法进行证明即可;(2)由(1)可得an=n+1,从而有 ![]() =(n+1)n , 利用二项式定理展开式以及构造函数,利用单调性证明.
=(n+1)n , 利用二项式定理展开式以及构造函数,利用单调性证明.
【考点精析】通过灵活运用数列的通项公式和数学归纳法的定义,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式;数学归纳法是证明关于正整数n的命题的一种方法即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,已知AB为圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦AG交CD于F.
(1)求证:E,F,G,B四点共圆;
(2)若GF=2FA=4,求线段AC的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一点在直线上从时刻t=0(s)开始以速度v(t)=t2﹣4t+3(m/s)运动,求:
(1)在t=4s时的位置;
(2)在t=4s的运动路程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1 , CC1上,且C1F= ![]() C1C,BE=λBB1 , 0<λ<1.
C1C,BE=λBB1 , 0<λ<1. 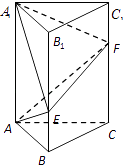
(1)当λ= ![]() 时,求异面直线AE与A1F所成角的大小;
时,求异面直线AE与A1F所成角的大小;
(2)当直线AA1与平面AEF所成角的正弦值为 ![]() 时,求λ的值.
时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以原点为圆心,椭圆的焦距为直径的圆与直线
,且以原点为圆心,椭圆的焦距为直径的圆与直线![]() 相切(
相切(![]() 为常数).
为常数).

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,若椭圆的![]() 左、右焦点分别为
左、右焦点分别为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆分别交于两点
与椭圆分别交于两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com