
(1)-1,1,-2,2,-3,3,…;(2)9,99,999,9 999,….
思路分析:写出数列的通项公式,应注意观察数列中各项和项数n的联系和变化情况,应特别注意自然数列、正奇数列、正偶数列,(-1)n和相关数列,等差、等比以及由它们组成的数列,从中找出规律性,并分别写出通项公式.
解:(1)∵所有奇数项上的数组成数列-1,-2,-3,…;所有偶数项上的数组成数列1,2,3,…,
∴分别求通项后得
an=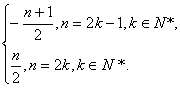
(2)∵9=10-1,99=102-1,999=103-1,…,![]() =10n-1,
=10n-1,
∴原数列变为10-1,102-1,103-1,….
∴an=10n-1.
温馨提示
此例可推广为:(1)5,55,555,…,an=![]() (10n-1);(2)7,77,777,…,an=
(10n-1);(2)7,77,777,…,an=![]() (10n-1).
(10n-1).


科目:高中数学 来源:2010-2011学年湖北省孝感市英才高中高一(下)第一次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com