
分析 (Ⅰ)根据使得函数有意义的条件得到不等式解之即可;
(Ⅱ)根据奇偶函数的定义,判断f(-x)与f(x)的关系;
(Ⅲ)由f(x)=-$\frac{5}{3}$得到方程解之.
解答 解:(Ⅰ)由已知要使解析式有意义,则2x-1≠0,解得x≠0,所以函数的定义域为{x|x≠0}….(4分)
(Ⅱ)奇函数.因为f(-x)=$\frac{{2}^{-x}+1}{{2}^{-x}-1}=\frac{{2}^{x}+1}{1-{2}^{x}}$=-f(x);(10分)
(Ⅲ)由f(x)=-$\frac{5}{3}$,得到$\frac{{{2^x}+1}}{{{2^x}-1}}=-\frac{5}{3}$,∴${2^x}=\frac{1}{4}$,所以x=-2….(14分)
点评 本题考查了求函数的定义域,判断函数的奇偶性.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
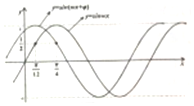
| A. | 沿x轴向左平移$\frac{π}{6}$个单位 | B. | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C. | 沿x轴向右平移$\frac{π}{6}$个单位 | D. | 沿x轴向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com