
设奇函数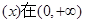 上是增函数,且
上是增函数,且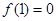 ,则不等式
,则不等式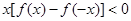 的解集为( )
的解集为( )
A.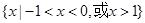 B.
B.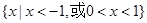
C.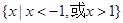 D.
D.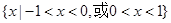
D
【解析】
试题分析:由题意可知,函数f(x)是奇函数,函数f(x)在(0,+∞)上是增函数,∴它在(-∞,0)上也是增函数.∵f(-x)=-f(x),∴f(-1)=f(1)=0.不等式x[f(x)-f(-x)]<0可化为2xf(x)<0,即xf(x)<0,∴当x<0时,可得f(x)>0=f(-1),∴x>-1,∴-1<x<0;当x>0时,可得f(x)<0=f(1),∴x<1,∴0<x<1.综上,
不等式x[f(x)-f(-x)]<0的解集为{x|-1<x0,或0<x<1}.故选D.
考点:本试题主要考查了是函数的奇偶性和单调性以及解不等式的综合类问题.在解答的过程当中充分体现了转化的思想、数形结合的思想以及函数单调性与奇偶性的知识.值得同学们体会和反思.
点评:解决该试题的关键要结合奇偶性和单调性对不等式进行转化变形,将问题转化为解不等式:2xf(x)<0,然后再分类讨论即可获得问题的解答。


科目:高中数学 来源:2014届浙江省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
设奇函数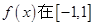 上是增函数,且
上是增函数,且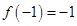 ,若函数
,若函数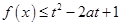 对所有的
对所有的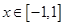 都成立,则当
都成立,则当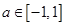 时t的取值范围是 ( )
时t的取值范围是 ( )
A.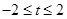 B.
B.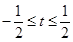
C.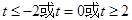 D.
D.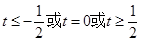
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市长河高三市二测模考数学文卷 题型:填空题
. 设奇函数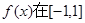 上是增函数,且
上是增函数,且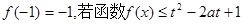 对所有的
对所有的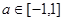 ,
,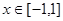 都成立,则t的取值范围是________________.
都成立,则t的取值范围是________________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三9月月考数学卷 题型:选择题
设奇函数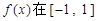 上是增函数,且
上是增函数,且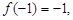 若函数
若函数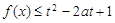 对所有的
对所有的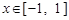 都成立,当
都成立,当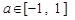 时,则t的取值范围是 ( )
时,则t的取值范围是 ( )
A.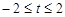 B.
B.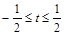
C.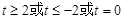 D.
D.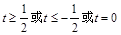
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com