
【题目】两个函数![]() 在公共定义域上恒有
在公共定义域上恒有![]() ,则称这两个函数是该区间上的“同步函数”.
,则称这两个函数是该区间上的“同步函数”.
(1)试判断![]() 与
与![]() 是否为公共定义域上的“同步函数”?
是否为公共定义域上的“同步函数”?
(2)已知函数![]() 与
与![]() 是公共区域上的“同步函数”,求实数
是公共区域上的“同步函数”,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 与
与![]() 在
在![]() 上是“同步函数”,求实数
上是“同步函数”,求实数![]() 的取值范围。
的取值范围。
【答案】(1)不是;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)由反正弦函数的定义域和值域、指数函数的单调性,结合新定义即可判断;
(2)分别讨论![]() ,
,![]() 对应方程的系数是否成比例,以及判别式的符号,解不等式,结合新定义,即可得到所求范围;
对应方程的系数是否成比例,以及判别式的符号,解不等式,结合新定义,即可得到所求范围;
(3)运用对数函数的定义域可得![]() ,求得
,求得![]() ,
,![]() 的零点,由于
的零点,由于![]() ,讨论当
,讨论当![]() 时,当
时,当![]() 时,当
时,当![]() 时,由不等式的性质即可得到所求范围.
时,由不等式的性质即可得到所求范围.
(1)![]() 在
在![]() 递增,
递增,![]() 在
在![]() 递减,
递减,
当![]() 时,
时,![]() ,而
,而![]() 在
在![]() 时,
时,![]() ,不满足
,不满足![]() ,
,
故![]() 与
与![]() 不为公共定义域上的“同步函数”;
不为公共定义域上的“同步函数”;
(2)由![]() 与
与![]() 是公共区域上的“同步函数”,
是公共区域上的“同步函数”,
可得在公共定义域上![]() ,
,
若![]() ,
,![]() 对应的方程是同解方程,
对应的方程是同解方程,
则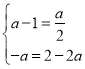 ,解得
,解得![]() .
.
此![]() .
.
若![]() ,
,![]() 对应的方程不是同解方程,
对应的方程不是同解方程,
要保证对于定义域内的任意实数![]() ,函数值乘积均为正,
,函数值乘积均为正,
则需要分子分母的判别式均小于![]() ,
,
即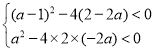 ,
,
解得![]() .
.
![]()
![]() 的范围是
的范围是![]() .
.
当![]() 时,函数化为
时,函数化为![]() 与
与![]() ,
,
![]() 大于等于
大于等于![]() ,
,![]() 的判别式小于
的判别式小于![]() ,
,![]() 大于
大于![]() 恒成立,函数值乘积恒非负.
恒成立,函数值乘积恒非负.
综上,则实数a的取值范围是![]() 或
或![]() ;
;
(3)由定义域可得![]() ,由题意可得
,由题意可得![]() ,
,
由![]() ,可得
,可得![]() ,
,
由![]() ,可得
,可得![]() ,
,
由题意可得两零点之间无正整数,
由于![]() ,所以当
,所以当![]() 时,
时,![]() ,不满足题意;
,不满足题意;
当![]() 时,
时,![]() ,不满足题意;
,不满足题意;
当![]() 时,
时,![]() ,满足题意.
,满足题意.
则![]() 的范围是
的范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() ,
,![]() 满足:
满足:![]() ,且
,且![]() ,
,![]() ,并且当
,并且当![]() 时,
时,![]() .给出如下结论:①函数
.给出如下结论:①函数![]() 是偶函数;②函数
是偶函数;②函数![]() 在
在![]() 上单调递增;③函数
上单调递增;③函数![]() 是以2为周期的周期函数;④
是以2为周期的周期函数;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校理科实验班的100名学生期中考试的语文、数学成绩都不低于100分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:[100,110),[110,120),[120,130),[130,140),[140,150].
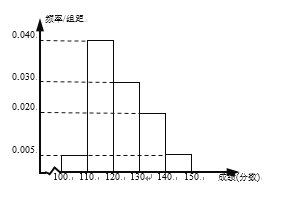
这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 | [100,110) | [110,120) | [120,130) | [130,140) |
| 1:2 | 2:1 | 3:4 | 1:1 |
(1)估计这100名学生语文成绩的平均数、方差(同一组数据用该区间的中点值作代表);
(2)从数学成绩在[130,150] 的学生中随机选取2人,该2人中数学成绩在[140,150]的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为![]() 公里,远月点与月球表面距离为
公里,远月点与月球表面距离为![]() 公里.已知月球的直径为
公里.已知月球的直径为![]() 公里,则该椭圆形轨道的离心率约为
公里,则该椭圆形轨道的离心率约为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com