
【题目】在平面直角坐标系xOy中,点![]() 满足方程
满足方程![]() .
.
(1)求点M的轨迹C的方程;
(2)作曲线C关于![]() 轴对称的曲线,记为
轴对称的曲线,记为![]() ,在曲线C上任取一点
,在曲线C上任取一点![]() ,过点P作曲线C的切线l,若切线l与曲线
,过点P作曲线C的切线l,若切线l与曲线![]() 交于A,B两点,过点A,B分别作曲线
交于A,B两点,过点A,B分别作曲线![]() 的切线
的切线![]() ,
,![]() ,且
,且![]() ,
,![]() 的交点为Q,试问以Q为直角的
的交点为Q,试问以Q为直角的![]() 是否存在,若存在,求出点P的坐标;若不存在,请说明理由.
是否存在,若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ,(2)存在,
,(2)存在,![]() 或
或![]()
【解析】
(1)平方化简![]() ,即可求解;
,即可求解;
(2)根据导数的几何意义求出切线l的方程,与曲线![]() 方程联立,由韦达定理,确定两交点A,B坐标关系,再利用导数的几何意义,求出切线
方程联立,由韦达定理,确定两交点A,B坐标关系,再利用导数的几何意义,求出切线![]() ,
,![]() 的方程,并联立求出Q点坐标,
的方程,并联立求出Q点坐标,
利用![]() ,结合A,B坐标关系,即可求解.
,结合A,B坐标关系,即可求解.
(1)由![]() ,
,
两边平方并化简,得![]() ,即
,即![]() ,
,
所以点M的轨迹C的方程为![]() .
.
(2)依题可设点![]() ,
,![]() ,
,
曲线C切于点P的切线l的斜率为![]() ,
,
切线l的方程为![]() ,
,
整理得![]()
依题可知曲线![]() ,
,
联立方程组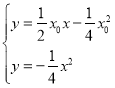
![]() ,
,![]() ,
,
设![]() ,
,![]() ,所以
,所以![]() ,
,![]() .(*)
.(*)
设曲线![]() 上点
上点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
切线方程为![]() ,整理得
,整理得![]() ,
,
同理可得曲线![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,
,
联立方程组 ,
,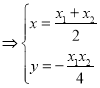 ,
,
又由(*)式得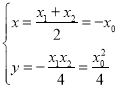 ,
,
所以![]() ,
,![]() 的交点Q的坐标为
的交点Q的坐标为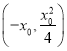 ,
,
假设以Q为直角的![]() 存在,则有
存在,则有![]() ,
,
而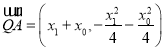 ,
,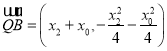 ,
,
所以由![]() ,得
,得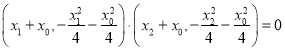 ,
,
即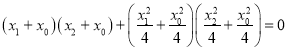 ,
,
即![]() ,
,
化简得![]() ,
,
因为由题得![]() ,所以
,所以![]() 或
或![]() ,
,
所以点P的坐标为![]() 或
或![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=
=1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=![]() ,△BF1F2为直角三角形.
,△BF1F2为直角三角形.
(1)求椭圆C的方程;
(2)设直线y=kx+2与椭圆交于P、Q两点,且OP⊥OQ,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况,该州教育局组织高三理科生进行了摸底考试,现从参加考试的学生中随机抽取了100名理科生,,将他们的化学成绩(满分为100分)分为![]()
![]()
![]()
![]()
![]()
![]() 6组,得到如图所示的频率分布直方图.
6组,得到如图所示的频率分布直方图.

(1)求a的值;
(2)记A表示事件“从参加考试的所有理科生中随机抽取一名学生,该学生的化学成绩不低于70分”,试估计事件A发生的概率;
(3)在抽取的100名理科生中,采用分层抽样的方法从成绩在![]() 内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在
内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在![]() 内的人数为X,求X的分布列与数学期望.
内的人数为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:,
![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,左焦点
,左焦点![]()
(1)求椭圆C的标准方程;
(2)过点F作于x轴不重合的直线l,l与椭圆交于A,B两点,点A在直线![]() 上的投影N与点B的连线交x轴于D点,D点的横坐标
上的投影N与点B的连线交x轴于D点,D点的横坐标![]() 是否为定值?若是,请求出定值;若不是,请说明理由
是否为定值?若是,请求出定值;若不是,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,
为其焦点,![]() 为其准线,过
为其准线,过![]() 任作一条直线交抛物线于
任作一条直线交抛物线于![]() 两点,
两点,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 为
为![]() 的中点,给出下列命题:
的中点,给出下列命题:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 与
与![]() 的交点的
的交点的![]() 轴上;(5)
轴上;(5)![]() 与
与![]() 交于原点.
交于原点.
其中真命题的序号为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在正常数
,若存在正常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立,我们称函数
成立,我们称函数![]() 为“
为“![]() 同比不减函数”.
同比不减函数”.
(1)求证:对任意正常数![]() ,
,![]() 都不是“
都不是“![]() 同比不减函数”;
同比不减函数”;
(2)若函数![]() 是“
是“![]() 同比不减函数”,求
同比不减函数”,求![]() 的取值范围;
的取值范围;
(3)是否存在正常数![]() ,使得函数
,使得函数![]() 为“
为“![]() 同比不减函数”,若存在,求
同比不减函数”,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
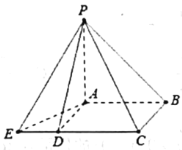
【题目】中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,若鳖臑
,若鳖臑![]() 的外接球的体积为
的外接球的体积为![]() ,则阳马
,则阳马![]() 的外接球的表面积等于______。
的外接球的表面积等于______。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com