
【题目】下列选项中,说法正确的是( )
A.命题“?x0∈R,x02﹣x0≤0”的否定为“?x∈R,x2﹣x>0”
B.命题“在△ABC中,A>30°,则sinA> ![]() ”的逆否命题为真命题
”的逆否命题为真命题
C.设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件
D.若非零向量 ![]() 、
、 ![]() 满足|
满足| ![]() +
+ ![]() |=|
|=| ![]() |+|
|+| ![]() |,则
|,则 ![]() 与
与 ![]() 共线
共线
【答案】D
【解析】解:对于A,由特称命题的否定为全称命题,可得命题“x0∈R,x02﹣x0≤0” 的否定为“x∈R,x2﹣x>0”,故A错;
对于B,命题“在△ABC中,A>30°,则sinA> ![]() ”为假命题,比如A=150°,则sinA=
”为假命题,比如A=150°,则sinA= ![]() .
.
再由原命题与其逆否命题等价,则其逆否命题为假命题,故B错;
对于C,设{an}是公比为q的等比数列,则“q>1”推不出“{an}为递增数列”,比如a1<0,不为增函数;
反之,可得0<q<1.故不为充分必要条件,故C错;
对于D,若非零向量 ![]() 、
、 ![]() 满足|
满足| ![]() +
+ ![]() |=|
|=| ![]() |+|
|+| ![]() |,则
|,则 ![]() ,
, ![]() 同向,则
同向,则 ![]() 与
与 ![]() 共线,故D正确.
共线,故D正确.
故选:D.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,离心率为
,离心率为![]() ,并过点
,并过点![]() .
.
(1)求椭圆方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点(
两点(![]() 不是左右顶点),且以
不是左右顶点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点。求证:直线
的右顶点。求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和,已知a1=1,an+1=2Sn+1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() =3n﹣1,求数列{bn}的前n项和Tn .
=3n﹣1,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 为n个正数
为n个正数![]() 的“均倒数”.已知正项数列{an}的前n项的“均倒数”为
的“均倒数”.已知正项数列{an}的前n项的“均倒数”为![]() .
.
(1)求数列{an}的通项公式.
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若4
,若4![]() <
<![]() 对一切
对一切![]() 恒成立试求实数m的取值范围.
恒成立试求实数m的取值范围.
(3)令![]() ,问:是否存在正整数k使得
,问:是否存在正整数k使得![]() 对一切
对一切![]() 恒成立,如存在求出k值,否则说明理由.
恒成立,如存在求出k值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下面材料,完成数学问题.
我校高二文科班的同学到武昌农民运动讲习所研学的途中路过武汉长江大桥边的武昌长江大堤,同学们在大堤上看到与武昌隔江相对的汉阳龟山上的电视塔和汉阳江边的晴川饭店在朝阳的映照下显得非常美丽,纷纷拿出手机拍照。这时带队的老师问大家,我要站在武昌大堤的哪一点才能够同时拍下电视塔和晴川饭店最清晰的图像?听到这个问题后,同学们议论纷纷。讨论一会后,一个同学对大家说:“把电视塔看成点A,饭店看成点B,武昌大堤看成直线l,C是直线l上的动点,拍照最佳点就是直线上使∠ACB最大的点.使∠ACB最大的点的求法用初中数学的一个定理:过点A,B作与直线l相切的圆,半径较小的圆和直线l的切点就是直线l上使∠ACB最大的点。”老师和同学们听了拍手称对。回到学校后,一位同学利用百度地图测距功能测得点A到直线l距离是2km,点B到直线l距离是1.5km,A,B两点间的距离是1km.该同学以直线l为x轴,过A点和直线l垂直的直线为y轴建立了如图所示的坐标系,点A的坐标为(0, 2),点B在第一象限.根据以上材料,请在所给的坐标系中,在x轴上求使∠ACB最大的点的坐标.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() (a>b>0)的左、右焦点F1、F2 , 其离心率e=
(a>b>0)的左、右焦点F1、F2 , 其离心率e= ![]() ,且点F2到直线
,且点F2到直线 ![]() =1的距离为
=1的距离为 ![]() .
.
(1)求椭圆E的方程;
(2)设点P(x0 , y0)是椭圆E上的一点(x0≥1),过点P作圆(x+1)2+y2=1的两条切线,切线与y轴交于A、B两点,求|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①垂直于同一条直线的两条直线平行;
②垂直于同一条直线的两个平面平行;
③垂直于同一平面的两个平面平行;
④垂直于同一平面的两条直线平行.
其中正确的命题有(填写所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD= ![]() ,则直线AD与平面BCD所成角的大小是( )
,则直线AD与平面BCD所成角的大小是( ) 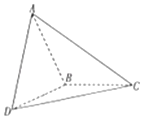
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com