
【题目】已知椭圆C的中心在原点,一个焦点为![]() ,且长轴与短轴长的比是
,且长轴与短轴长的比是![]()
(1)求椭圆C的方程;
(2)设点![]() 在 椭圆C的长轴上,点P是椭圆上任意一点,当
在 椭圆C的长轴上,点P是椭圆上任意一点,当![]() 最小时,点P恰好落在椭圆的右顶点上,求实数
最小时,点P恰好落在椭圆的右顶点上,求实数![]() 的取值范围.
的取值范围.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知边长为![]() 米的正方形钢板有一个角被锈蚀,其中
米的正方形钢板有一个角被锈蚀,其中![]() 米,
米, ![]() 米.为了合理利用这块钢板,将在五边形
米.为了合理利用这块钢板,将在五边形![]() 内截取一个矩形块
内截取一个矩形块![]() ,使点
,使点![]() 在边
在边![]() 上.
上.
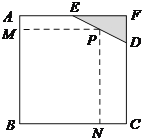
(1)设![]() 米,
米, ![]() 米,将
米,将![]() 表示成
表示成![]() 的函数,求该函数的解析式及定义域;
的函数,求该函数的解析式及定义域;
(2)求矩形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设![]() 为两个同高的几何体,
为两个同高的几何体,![]() 的体积不相等,
的体积不相等,![]() 在等高处的截面积不恒相等,根据祖暅原理可知,
在等高处的截面积不恒相等,根据祖暅原理可知,![]() 是
是![]() 的( )
的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列集合间的关系:
(1)A={x|x-3>2},B={x|2x-5≥0};
(2)A={x∈Z|-1≤x<3},B={x|x=|y|,y∈A}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
x | … | 30 | 40 | 45 | 50 | … |
y | … | 60 | 30 | 15 | 0 | … |
(1)在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x);
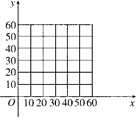
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,它在点
,它在点![]() 处的切线为直线
处的切线为直线![]() .
.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 为椭圆
为椭圆![]() 上一点,求点
上一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市将建一个制药厂,但该厂投产后预计每天要排放大约80吨工业废气,这将造成极大的环境污染.为了保护环境,市政府决定支持该厂贷款引进废气处理设备来减少废气的排放,该设备可以将废气转化为某种化工产品和符合排放要求的气体,经测算,制药厂每天利用设备处理废气的综合成本![]() (元)与废气处理量
(元)与废气处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理
,且每处理![]() 吨工业废气可得价值为
吨工业废气可得价值为![]() 元的某种化工产品并将之利润全部用来补贴废气处理.
元的某种化工产品并将之利润全部用来补贴废气处理.
(1)若该制药厂每天废气处理量计划定位20吨时,那么工厂需要每天投入的废气处理资金为多少元?
(2)若该制药厂每天废气处理量计划定为![]() 吨,且工厂不用投入废气处理资金就能完成计划的处理量,求
吨,且工厂不用投入废气处理资金就能完成计划的处理量,求![]() 的取值范围;
的取值范围;
(3)若该制药厂每天废气处理量计划定为![]() (
(![]() )吨,且市政府决定为处理每吨废气至少补贴制药厂
)吨,且市政府决定为处理每吨废气至少补贴制药厂![]() 元以确保该厂完成计划的处理量总是不用投入废气处理资金,求
元以确保该厂完成计划的处理量总是不用投入废气处理资金,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com