
【题目】设函数f(x)= ![]() (a>b>0)的图象是曲线C.
(a>b>0)的图象是曲线C. 
(1)在如图的坐标系中分别做出曲线C的示意图,并分别标出曲线C与x轴的左、右交点A1 , A2 .
(2)设P是曲线C上位于第一象限的任意一点,过A2作A2R⊥A1P于R,设A2R与曲线C交于Q,求直线PQ斜率的取值范围.
【答案】
(1)解:∵f(x)= ![]() (a>b>0),
(a>b>0),
∴y= ![]() ,
,
∴a2y2=b2(a2﹣x2),∴b2x2+a2y2=b2a2,
∴ ![]() =1,a>b>0,且y≥0,
=1,a>b>0,且y≥0,
其图象表示焦点在x轴上椭圆的一部分,
如图所示,A1 (﹣a,0)、A2(a,0)
(2)解:曲线C的方程是 ![]() =1(a>b>0,y≥0),
=1(a>b>0,y≥0),
设 直线A1P的斜率是k,
因为P是曲线C上位于第一象限内的任意一点,所以k∈(0, ![]() ).
).
设P,Q的坐标分别是(x1,y1),(x2,y2),则直线A1P的方程是y=k(x+a),
由 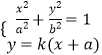 消去y得,(a2k2+b2)x2+2a3k2x+a2(a2k2﹣b2)=0,
消去y得,(a2k2+b2)x2+2a3k2x+a2(a2k2﹣b2)=0,
解得x1= ![]() ,y1=
,y1= ![]() .
.
将上式中的a换成﹣a,k换成﹣ ![]() 得x2=
得x2= ![]() ,y2=
,y2= ![]() ,
,
∴KPQ= ![]() =
= ![]() (k﹣
(k﹣ ![]() ),由于y=
),由于y= ![]() (k﹣
(k﹣ ![]() )在∈(0,
)在∈(0, ![]() )上单调递增,
)上单调递增,
∴KPQ= ![]() =
= ![]() (k﹣
(k﹣ ![]() )<
)< ![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]() ,
,
故直线PQ斜率的取值范围为(﹣∞, ![]() ).
).
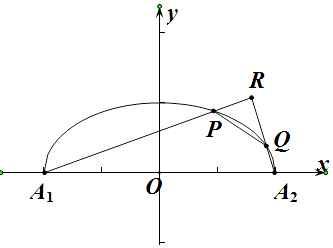
【解析】(1)化简函数的解析式为 ![]() =1,a>b>0,且y≥0,其图象表示焦点在x轴上椭圆的一部分,数形结合求得,A1 和A2的坐标.(2)先考察一般性,直线A1P的方程是y=k(x+a),与椭圆方程联立,求得P,Q的坐标,可得直线PQ斜率,即可求出取值范围.
=1,a>b>0,且y≥0,其图象表示焦点在x轴上椭圆的一部分,数形结合求得,A1 和A2的坐标.(2)先考察一般性,直线A1P的方程是y=k(x+a),与椭圆方程联立,求得P,Q的坐标,可得直线PQ斜率,即可求出取值范围.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+2a2+3a3+…+nan=n(n∈N*).
(1)求数列{an}的通项公式an;
(2)令 ![]() ,写出Tn关于n的表达式,并求满足Tn>
,写出Tn关于n的表达式,并求满足Tn> ![]() 时n的取值范围.
时n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为
精确到0.1),若某天的气温为![]() ,预测这天热奶茶的销售杯数;
,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取两天,求所选取两天中至少有一天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=﹣xn+3ax(a∈R,n∈N+),若对任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,则a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
![]()
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到一个奇函数,只需将函数f(x)=sin2x﹣ ![]() cos2x的图象( )
cos2x的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示. 
(1)求A,ω,φ的值;
(2)设θ为锐角,且f(θ)=﹣ ![]() ,求f(θ﹣
,求f(θ﹣ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com