
△ABC的三个内角A、B、C的对边的长分别为a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)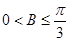 ;(2)
;(2)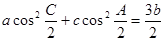 ;(3)
;(3)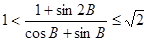 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①__________________________________________
②__________________________________________
(II)证明:
略
【解析】可以组建命题一:△ABC中,若a、b、c成等差数列,求证:(1)0<B≤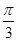
(2)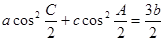 ;
;
命题二:△ABC中,若a、b、c成等差数列求证:(1)0<B≤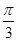
(2)1<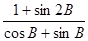 ≤
≤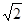
命题三:△ABC中,若a、b、c成等差数列,求证:(1)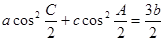
(2)1<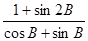 ≤
≤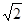
命题四:△ABC中,若a、b、c成等比数列,求证:(1)0<B≤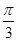
(2)1<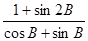 ≤
≤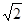 [来源:学。科。网]
[来源:学。科。网]
下面给出命题一、二、三的证明:
(1)∵a、b、c成等差数列∴2b=a+c,∴b=
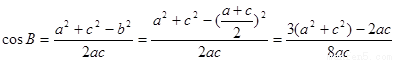 ≥
≥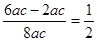
且B∈(0,π),∴0<B≤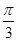
(2)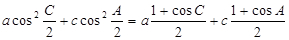
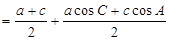
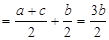
(3)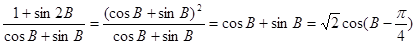
∵0<B≤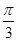 ∴
∴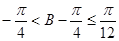 ∴
∴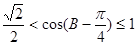
∴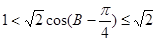
下面给出命题四的证明:
(4)∵a、b、c成等比数列∴b2=a+c,
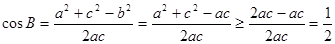
且B∈(0,π),∴0<B≤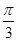


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com