
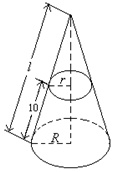
 把一个圆锥截成圆台,已知圆台的上、下底面半径分别为1cm、4cm,母线长10cm.
把一个圆锥截成圆台,已知圆台的上、下底面半径分别为1cm、4cm,母线长10cm.分析 (1)确定圆锥的母线长为L,截得小圆锥的母线长为l的关系,即可求出圆锥的母线长;
(2)利用公式圆台表面积;
(3)圆台的高为$\sqrt{100-9}$=$\sqrt{91}$,利用公式求出圆台体积.
解答 解:(1)设圆锥的母线长为L,截得小圆锥的母线长为l,
∵圆台的上、下底面互相平行,圆台的上、下底面半径分别为1cm、4cm
∴可得L=4l
∵圆台的母线长10cm,可得L-l=10cm
∴$\frac{3}{4}$L=10cm,解得L=$\frac{40}{3}$cm;
(2)圆台表面积S=π•(1+4)•10=50πcm2;
(3)圆台的高为$\sqrt{100-9}$=$\sqrt{91}$,圆台体积$\frac{\sqrt{91}π}{3}(1+16+4)$=$7\sqrt{91}πc{m}^{3}$.
点评 本题考查了圆锥的平行截面的性质、圆台定义及应用等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
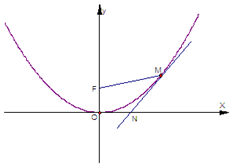 如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.
如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com