
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() .使得函数
.使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() 若存在,求实数
若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() 时,
时,![]() 在
在![]() 单调增;
单调增;![]() 时,
时, ![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;![]() 时,同理
时,同理![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;(3)不存在.
单调递增;(3)不存在.
【解析】分析:(1)利用导数研究函数的单调性,可得当![]() 时,
时, ![]() 取得极大值,也是最大值,
取得极大值,也是最大值,
由![]() ,可得结果;(2)求出
,可得结果;(2)求出![]() ,分三种情况讨论
,分三种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(3)假设存在区间
的减区间;(3)假设存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() ,则
,则![]() ,问题转化为关于
,问题转化为关于![]() 的方程
的方程![]() 在区间
在区间![]() 内是否存在两个不相等的实根,进而可得结果.
内是否存在两个不相等的实根,进而可得结果.
详解:(1) 由题意得![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() 取得极大值,也是最大值,
取得极大值,也是最大值,
所以![]() ,解得
,解得![]() .
.
(2)![]() 的定义域为
的定义域为![]() .
.
![]()
①![]() 即
即![]() ,则
,则![]() ,故
,故![]() 在
在![]() 单调增
单调增
②若![]() ,而
,而![]() ,故
,故![]() ,则当
,则当![]() 时,
时,![]() ;
;
当![]() 及
及![]() 时,
时,![]()
故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增。
单调递增。
③若![]() ,即
,即![]() ,同理
,同理![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
(3)由(1)知![]() ,
,
所以![]() ,令
,令![]() ,则
,则![]() 对
对![]() 恒成立,所以
恒成立,所以![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() 恒成立,
恒成立,
所以函数![]() 在区间
在区间![]() 内单调递增.
内单调递增.
假设存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() ,
,
则![]() ,
,
问题转化为关于![]() 的方程
的方程![]() 在区间
在区间![]() 内是否存在两个不相等的实根, 即方程
内是否存在两个不相等的实根, 即方程![]() 在区间
在区间![]() 内是否存在两个不相等的实根,
内是否存在两个不相等的实根,
令![]() ,
, ![]() ,则
,则![]() ,
,
设![]() ,
, ![]() ,则
,则![]() 对
对![]() 恒成立,所以函数
恒成立,所以函数![]() 在区间
在区间![]() 内单调递增,
内单调递增,
故![]() 恒成立,所以
恒成立,所以![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 内单调递增,所以方程
内单调递增,所以方程![]() 在区间
在区间![]() 内不存在两个不相等的实根.
内不存在两个不相等的实根.
综上所述,不存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域是
上的值域是.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】已知点P(-1,0),设不垂直于x轴的直线l与抛物线y2=2x交于不同的两点A、B,若x轴是∠APB的角平分线,则直线l一定过点
A. (![]() ,0) B. (1,0) C. (2,0) D. (-2,0)
,0) B. (1,0) C. (2,0) D. (-2,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() 两款车扩大市场,
两款车扩大市场, ![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:
车型 | 报废年限(年) | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入![]() 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数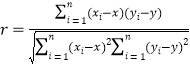 ;
;
回归直线方程为![]() ,其中
,其中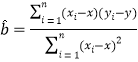 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求第四小组的频率,并补全频率分布直方图;
(2)根据频率分布直方图估计这次考试的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com