
【题目】设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为 ![]() ,则实数a的值为( )
,则实数a的值为( )
A.![]()
B.![]() 或
或 ![]()
C.![]()
D.![]() 或
或 ![]()
【答案】C
【解析】解:函数f(x)=|logax|在(0,1)递减,在[1,+∞)递增 ∵值域为[0,1],n﹣m要最小值∴定义域为[a,1]或[1, ![]() ]
]
∵ ![]() ﹣1=
﹣1= ![]() >1﹣a,故定义域只能为[a,1];
>1﹣a,故定义域只能为[a,1];
∴n﹣m=1﹣a= ![]() 即 a=
即 a= ![]() .
.
故选C.
【考点精析】本题主要考查了函数的定义域及其求法和函数的值域的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示相等函数的一组是( )
A.f(x)=1,g(x)=x0?
B.f(x)=|x|,g(t)= ![]()
C.f(x)= ![]() ,g(x)=x+1?
,g(x)=x+1?
D.f(x)=lg(x+1)+lg(x﹣1),g(x)=lg(x2﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(2)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
假设花店在这![]() 天内每天购进
天内每天购进![]() 枝玫瑰花,求这
枝玫瑰花,求这![]() 天的日利润(单位:元)的平均数.
天的日利润(单位:元)的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,若存在常数T≠0,使得f(x)=Tf(x+T)对任意的x∈R成立,则称函数f(x)是Ω函数. (Ⅰ)判断函数f(x)=x,g(x)=sinπx是否是Ω函数;(只需写出结论)
(Ⅱ)说明:请在(i)、(ii)问中选择一问解答即可,两问都作答的按选择(i)计分
(i)求证:若函数f(x)是Ω函数,且f(x)是偶函数,则f(x)是周期函数;
(ii)求证:若函数f(x)是Ω函数,且f(x)是奇函数,则f(x)是周期函数;
(Ⅲ)求证:当a>1时,函数f(x)=ax一定是Ω函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() +c是奇函数,且满足f(1)=
+c是奇函数,且满足f(1)= ![]() ,f(2)=
,f(2)= ![]() .
.
(1)求a,b,c的值;
(2)试判断函数f(x)在区间(0, ![]() )上的单调性并证明.
)上的单调性并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且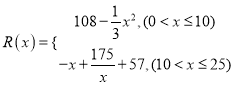 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com