练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给出以下命题：①“若x2+ y2 ≠0，则x，y不全为零”的否命题；②“正多边形都相似”的逆命题；③“若m>0，则x2+x-m=0有实根”的逆否命题；其中真命题的序号是____________

    【答案】①③

    【解析】

    ①“若x2+ y2 ≠0，则x，y不全为零”的否命题是若，则，都为零，它是真命题；②写出命题“正多边形都相似”的逆命题，然后判断它是假命题；③由“若，则有实根”是真命题，知它的逆否命题是真命题.

    对于①，其否命题为“若，则，都为零”，它是真命题，故①是真命题；

    对于②“正多边形都相似”的逆命题是：相似的多边形都是正多边形，所以②是假命题；

    对于③，时，，所以“若，则有实根”是真命题，

    它的逆否命题是真命题．即③是真命题；

    故答案为：①③．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

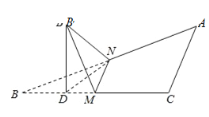
    【题目】如图，∠C=，AC=BC，M、N分别是BC、AB的中点，将△BMN沿直线MN折起，使二面角B′﹣MN﹣B的大小为，则B'N与平面ABC所成角的正切值是（ 　　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的一个焦点与抛物线：的焦点重合，且椭圆的离心率为．

    （1）求的方程；

    （2）过点的动直线与椭圆相交于两点，为原点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥P－ABCD中，底面ABCD为平行四边形，∠ADC＝45°，AD＝AC＝1，O为AC的中点，PO⊥平面ABCD，PO＝2，M为PD的中点．

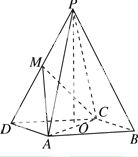
    （1）证明：PB∥平面ACM；

    （2）证明：AD⊥平面PAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正方体中，E、F、G、H分别为、BC、CD、BB、的中点，则下列结论正确的是（ ）

    A.B.平面平面

    C.面AEFD.二面角的大小为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为，直线的参数方程为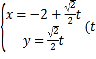为参数，直线与曲线分别交于两点.

    （1）若点的极坐标为，求的值；

    （2）求曲线的内接矩形周长的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn，等比数列{bn}的前n项和为Tn，a1＝1，b1＝﹣1，a2-b2＝2.

    （1）若a3-b3＝6，求{bn}的通项公式

    （2）若T3＝﹣13，求S5.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明设计了一款正四棱锥形状的包装盒，如图所示，是边长为的正方形硬纸片，切去阴影部分所示的四个全等的等腰三角形，再沿虚线折起，使得四个点重合于图中的点，正好形成一个正四棱锥形状的包装盒，设正四棱锥底面正方形的边长为.

    （1）试用表示该四棱锥的高度，并指出的取值范围；

    （2）若要求侧面积不小于，求该四棱锥的高度的最大值，并指出此时该包装盒的容积.

    查看答案和解析>>

    同步练习册答案