
【题目】求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(1)f(x)=-![]() ;
;
(2)f(x)=![]()
(3)f(x)=-x2+2|x|+3.
【答案】(1)单调区间为(-∞,0),(0,+∞),其在(-∞,0),(0,+∞)上都是增函数;(2)单调区间为(-∞,1),[1,+∞),并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数;(3)单调区间为(-∞,1),[1,+∞),并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数.
【解析】
(1)由反比例函数的图象,即可求出单调区间及单调性;
(2)由一次函数的图象特征,即可求出单调区间及单调性;
(3)去绝对值,分类讨论解析式,并做出分段函数的图象,根据图象求出单调区间及单调性.
(1)函数f(x)=-![]() 的单调区间为(-∞,0),(0,+∞),
的单调区间为(-∞,0),(0,+∞),
其在(-∞,0),(0,+∞)上都是增函数.
(2)当x≥1时,f(x)是增函数,当x<1时,f(x)是减函数,
所以f(x)的单调区间为(-∞,1),[1,+∞),
并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数.
(3)因为f(x)=-x2+2|x|+3=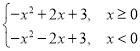
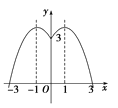
根据解析式可作出函数的图象如图所示,由图象可知,
函数f(x)的单调区间为(-∞,-1],(-1,0),[0,1),[1,+∞).
f(x)在(-∞,-1],[0,1)上是增函数,在(-1,0),[1,+∞)上是减函数.


科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
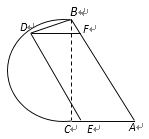
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,3a]上的最大值与最小值之差为1.
(1)求a的值;
(2)若1≤x≤3,求函数y=(logax)2-loga![]() +2的值域.
+2的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是某校高三(1)班的一次数学知识竞赛成绩的茎叶图(图中仅列出![]() ,
,![]() 的数据)和频率分布直方图.
的数据)和频率分布直方图.
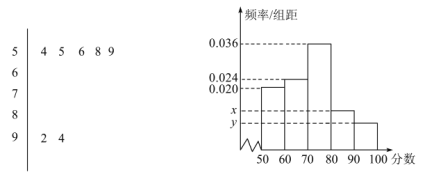
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求频率分布直方图中的![]() ;
;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
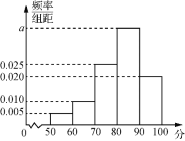
(1)求图中a的值;
(2)用样本估计总体,以频率作为概率,若在A,B两块试验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 过点P(-1,2),且倾斜角为
过点P(-1,2),且倾斜角为![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)设直线![]() 与圆
与圆![]() 交于M、N两点,求
交于M、N两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com