
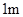 、
、 、
、 的钢管各
的钢管各 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取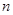 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,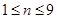 ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根. 时,记事件
时,记事件 {抽取的
{抽取的 根钢管中恰有
根钢管中恰有 根长度相等},求
根长度相等},求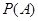 ;
; 时,若用
时,若用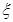 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求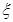 的分布列;
的分布列; ,
,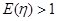 ,求实数
,求实数 的取值范围.
的取值范围. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 名网友的网购金额情况,得到如下数据统计表(如图):
名网友的网购金额情况,得到如下数据统计表(如图):
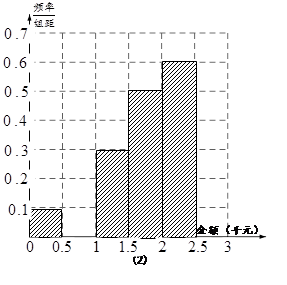
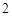 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过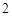 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为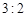 .
.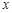 ,
,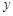 ,
,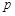 ,
,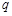 的值,并补全频率分布直方图(如图(2)).
的值,并补全频率分布直方图(如图(2)). 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定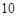 人,若需从这
人,若需从这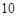 人中随机选取
人中随机选取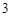 人进行问卷调查.设
人进行问卷调查.设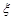 为选取的
为选取的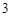 人中“网购达人”的人数,求
人中“网购达人”的人数,求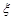 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
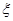 .
.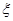 =6的概率;
=6的概率;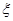 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
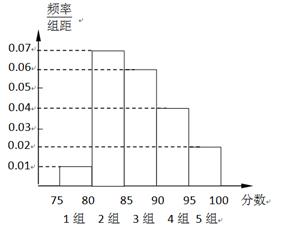
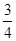 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有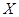 名获得优秀,求
名获得优秀,求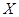 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
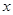 ,
,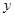 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:| 编号 | 1 | 2 | 3 | 4 | 5 |
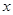 | 160 | 178 | 166 | 175 | 180 |
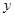 | 75 | 80 | 77 | 70 | 81 |
 且
且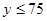 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数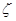 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
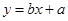 必过
必过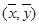
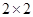 列联表中,由计算得
列联表中,由计算得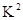 =4.235,则有95%的把握确认这两个变量间没有关系
=4.235,则有95%的把握确认这两个变量间没有关系 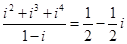
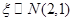 ,且p(
,且p(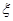 <4)=p,则p(0<
<4)=p,则p(0<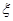 <2)=2p-1
<2)=2p-1| A.1 | B.2 | C.3 | D. 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com