
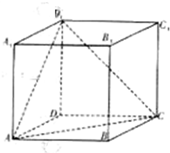
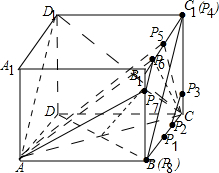
 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ4����P��B���������������BCC1B1�ı��ϰ����뷽�����¹����˶������n���˶���·��Ϊan����an=cos
��ͼ��������ABCD-A1B1C1D1���ⳤΪ4����P��B���������������BCC1B1�ı��ϰ����뷽�����¹����˶������n���˶���·��Ϊan����an=cos| n�� | 2 |
| n�� |
| 2 |
| n�� |
| 2 |
| AP5 |
| CP5 |
| AP6 |
| CP6 |
| a |
| c |
|
|
| a |
|
|
| c |
| b |
| ||||
|
|
| 1 |
| 3 |
| ||||
|
|
| 3 | ||
|
3
| ||
| 41 |
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 17 |
2
| ||
| 17 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪBB1��A1D1���е㣮֤��������
��ͼ��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪBB1��A1D1���е㣮֤��������| A1B |
| B1C |
| EF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��������ABCD-A1B1C1D1�ⳤΪ8��E��F�ֱ�ΪAD1��CD1�е㣬G��H�ֱ�Ϊ��DA��DC�϶��㣬��EH��FG��
��ͼ��������ABCD-A1B1C1D1�ⳤΪ8��E��F�ֱ�ΪAD1��CD1�е㣬G��H�ֱ�Ϊ��DA��DC�϶��㣬��EH��FG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��������ABCD-A1B1C1D1�У���E��F��G�ֱ�Ϊ��BC��C1C��B1C1���е㣬O1��O2�ֱ�Ϊ�ı���ADD1A1��A1B1C1D1�����ģ������и����е��ĸ��㲻��ͬһ��ƽ���ϵ��ǣ�������
��ͼ��������ABCD-A1B1C1D1�У���E��F��G�ֱ�Ϊ��BC��C1C��B1C1���е㣬O1��O2�ֱ�Ϊ�ı���ADD1A1��A1B1C1D1�����ģ������и����е��ĸ��㲻��ͬһ��ƽ���ϵ��ǣ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��������ABCD-A1B1C1D1�У�E��F��G��H�ֱ�������������ȷֵ㣬��BF=DE=C1G=C1H=
��ͼ��������ABCD-A1B1C1D1�У�E��F��G��H�ֱ�������������ȷֵ㣬��BF=DE=C1G=C1H=| 1 | 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com