
【题目】若函数![]() 对其定义域内的任意
对其定义域内的任意![]() ,
,![]() ,当
,当![]() 时总有
时总有![]() ,则称
,则称![]() 为紧密函数,例如函数
为紧密函数,例如函数![]() 是紧密函数,下列命题:
是紧密函数,下列命题:
![]() 紧密函数必是单调函数;
紧密函数必是单调函数;![]() 函数
函数![]() 在
在![]() 时是紧密函数;
时是紧密函数;
![]() 函数
函数![]() 是紧密函数;
是紧密函数;
![]() 若函数
若函数![]() 为定义域内的紧密函数,
为定义域内的紧密函数,![]() ,则
,则![]() ;
;
![]() 若函数
若函数![]() 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数![]() 在定义域内的值一定不为零.
在定义域内的值一定不为零.
其中的真命题是______.
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼游园工作,某单位设计了统计人数的数学模型![]() :以
:以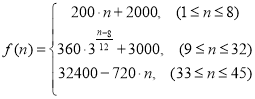 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以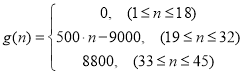 表示第
表示第![]() 个时刻离开园区的人数.设定以
个时刻离开园区的人数.设定以![]() 分钟为一个计算单位,上午
分钟为一个计算单位,上午![]() 点
点![]() 分作为第
分作为第![]() 个计算人数单位,即
个计算人数单位,即![]() ;
;![]() 点
点![]() 分作为第
分作为第![]() 个计算单位,即
个计算单位,即![]() ;依次类推,把一天内从上午
;依次类推,把一天内从上午![]() 点到晚上
点到晚上![]() 点
点![]() 分分成
分分成![]() 个计算单位(最后结果四舍五入,精确到整数).
个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天![]() 点至
点至![]() 点这一小时内,进入园区的游客人数
点这一小时内,进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]() 各为多少?
各为多少?
(2)假设当日园区游客总人数达到或超过![]() 万时,园区将采取限流措施.该单位借助该数学模型知晓当天
万时,园区将采取限流措施.该单位借助该数学模型知晓当天![]() 点(即
点(即![]() )时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
)时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() ,设
,设 .
.
(1)如果![]() 为奇函数,求实数
为奇函数,求实数![]() 、
、![]() 满足的条件;
满足的条件;
(2)在(1)的条件下,若函数![]() 在区间
在区间![]() 上为增函数,求
上为增函数,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() 恒有
恒有![]() 成立.证明:当
成立.证明:当![]() 时,
时,![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl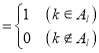 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(3)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() )的最小周期为
)的最小周期为![]() .
.
(1)求![]() 的值及
的值及![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标缩短为原来的
个单位,再将图象上各点的横坐标缩短为原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,若关于x的方程
的图象,若关于x的方程![]() 在区间
在区间![]() 上有且只有一个解,求实数m的取值范围.
上有且只有一个解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于自然数数组![]() ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果![]() 的极差
的极差![]() ,可实施如下操作
,可实施如下操作![]() :若
:若![]() 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若![]() 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为![]() ,其级差为
,其级差为![]() .若
.若![]() ,则继续对
,则继续对![]() 实施操作
实施操作![]() ,…,实施
,…,实施![]() 次操作后的结果记为
次操作后的结果记为![]() ,其极差记为
,其极差记为![]() .例如:
.例如:![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,若
,若![]() 时,恒有
时,恒有![]() ,求
,求![]() 的所有可能取值;
的所有可能取值;
(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,实数
,实数![]() 且
且![]() .
.
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)设![]() 且
且![]() 时,
时,![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,相邻两项an,an+1是关于x的方程:x2+3nx+bn![]() 0(n∈N*)的两实根,且a1=1.
0(n∈N*)的两实根,且a1=1.
(1)若Sn为数列{an}的前n项和,求S100 ;
(2)求数列{an}和{bn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com