
已知各项为正数的数列 满足
满足 (
( ),且
),且 是
是 的等差中项,则数列
的等差中项,则数列 的通项公式是 .
的通项公式是 .
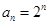
【解析】
试题分析:∵an+12-an+1an-2an2=0,∴(an+1+an)(an+1-2an)=0,∵数列{an}的各项均为正数,∴an+1+an>0,∴an+1-2an=0,即an+1=2an,所以数列{an}是以2为公比的等比数列.∵a3+2是a2,a4的等差中项,∴a2+a4=2a3+4,
∴2a1+8a1=8a1+4,∴a1=2,∴数列{an}的通项公式an=2n.
考点:本题考查了数量的递推关系
点评:数列是高中数学的重要内容,又是学习高等数学的基础,所以在高考中占有重要的地位.高考对本章的考查比较全面,等差数列,等比数列的考查每年都不会遗漏,属于中档题


科目:高中数学 来源: 题型:
| bn | an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2012届浙江省学军中学高三上学期理科数学期中考试试卷 题型:解答题
已知各项为正数的数列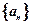 的前
的前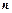 项和为
项和为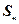 ,且满足
,且满足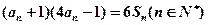 ,
,
(1)求数列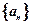 的通项公式
的通项公式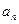
(2)令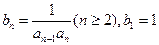 ,数列
,数列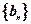 的前
的前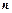 项和为
项和为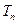 ,若
,若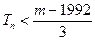 对一切
对一切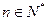 恒成立,求
恒成立,求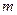 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期理科数学期中考试试卷 题型:解答题
已知各项为正数的数列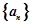 的前
的前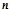 项和为
项和为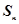 ,且满足
,且满足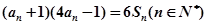 ,
,
(1)求数列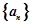 的通项公式
的通项公式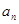
(2)令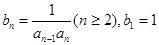 ,数列
,数列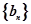 的前
的前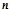 项和为
项和为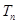 ,若
,若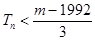 对一切
对一切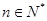 恒成立,求
恒成立,求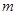 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com