
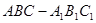 中,
中,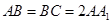
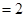 ,
,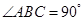 ,
,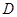 是
是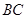 的中点.
的中点.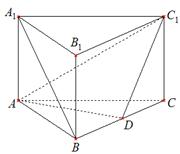
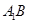 平行平面
平行平面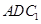 ;
;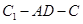 的余弦值;
的余弦值;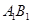 上是否存在点
上是否存在点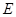 ,使
,使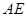 与
与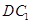 成
成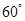 角?若存在,确定
角?若存在,确定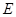 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.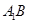 ∥
∥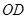 ;(2)
;(2)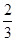 ;(3)点
;(3)点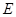 为线段
为线段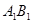 中点时,
中点时,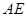 与
与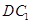 成
成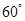 角.
角.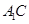 ,交
,交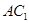 于点
于点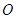 ,连结
,连结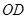 .
.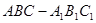 是直三棱柱,
是直三棱柱,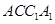 为矩形,
为矩形,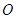 为
为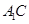 的中点.
的中点.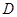 为
为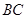 中点,所以
中点,所以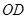 为
为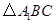 中位线,
中位线,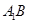 ∥
∥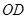 ,
, 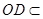 平面
平面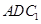 ,
,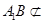 平面
平面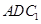 ,
, 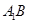 ∥平面
∥平面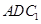 .
. 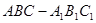 是直三棱柱,且
是直三棱柱,且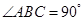 ,故
,故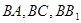 两两垂直.
两两垂直.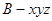 .设
.设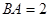 ,
,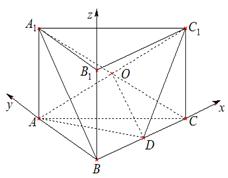
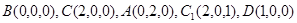 .
.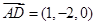 ,
,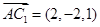
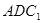 的法向量为
的法向量为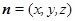 ,则有
,则有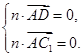
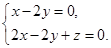 取
取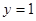 ,得
,得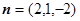 .
.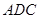 的法向量为
的法向量为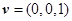 .
. 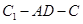 是锐角,得
是锐角,得 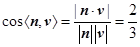 .
. 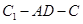 的余弦值为
的余弦值为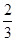 .
.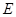 .
.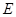 在线段
在线段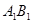 上,
上,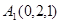 ,
,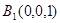 ,故可设
,故可设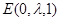 ,其中
,其中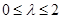 .
.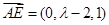 ,
,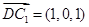 .
. 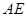 与
与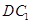 成
成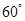 角,所以
角,所以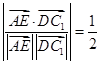 .
. 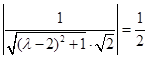 ,解得
,解得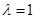 ,舍去
,舍去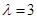 .
. 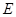 为线段
为线段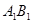 中点时,
中点时,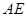 与
与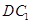 成
成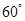 角.
角. 

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:不详 题型:解答题
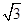 ,VA =" 6."
,VA =" 6." 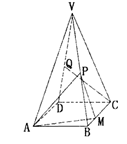
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 、
、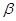 表示不同平面,下列命题正确的是 ( )
表示不同平面,下列命题正确的是 ( )A.若m‖ ,m‖ n,则n‖ ,m‖ n,则n‖ |
B.若m  ,n ,n  ,m‖ ,m‖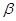 ,n‖ ,n‖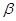 ,则 ,则 ‖ ‖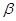 |
C.若 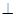 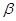 , m , m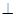  ,m ,m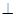 n,则n‖ n,则n‖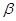 |
D.若 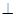 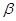 , m , m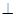  ,n‖m,n ,n‖m,n 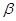 ,则n‖ ,则n‖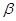 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
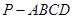 中,侧棱
中,侧棱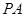 的长为
的长为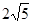 ,
,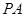 与
与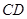 所成的角的大小等于
所成的角的大小等于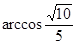 .
.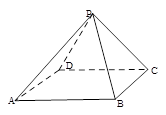
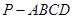 的体积;
的体积;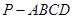 的五个顶点都在球
的五个顶点都在球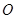 的表面上,求此球
的表面上,求此球 的半径.
的半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com