解:(Ⅰ)由题意,得2b
n2=a
n+a
n+1,①
a
n+12=b
n2b
n+12,②(1分)
因为a
n>0,b
n>0,所以由式②得a
n+1=b
nb
n+1,
从而当n≥2时,a
n=b
n-1b
n,
代入式①得2b
n2=b
n-1b
n+b
nb
n+1,(3分)
故当n≥2时,2b
n=b
n-1+b
n+1(n≥2),
∴数列b
n是等差数列.(4分)
(II)由
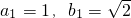
及式①、②易得
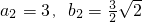
,
因此b
n 的公差

,
从而

,(5分)
得
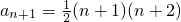
,
所以当n≥2时,

,③
又a
1=1也适合式③,
∴
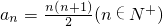
.(6分)
设P=2
n,Q=2n-n(n+1),
当n=1时,P=Q,当n=2,3,4时,P<Q
当n=5时,P>Q,当n=6时,P>Q
由此猜想当n≥5时,P>Q(8分)
以下用数学归纳法证明.
(1)当N=5时,P>Q显然成立,(9分)
(2)假设当n=k(k≥5)时,
P>Q成立,即2
n>k(k+1)-k
2+k成立,
则当n=k+1时,P=2
K+1=2•2
k>2k
2+2k
=(k
2+2k+1)+(k+1)+(k
2-k-2)=(k+1)
2+(k+1)+(k+1)(k-2)
∵k≥5,∴(k+1)(k-2)>0即P=2
k+1>(k+1)
2+(k+1)成立.
故当n=k+1时,P>Q成立.
由(1)、(2)得,当n≥5时,
P>Q成立.(11分)
因此,当n=1时,2
n=2a
n,
当n=2,3,4时,2
n<2a
n,
当n≥5时,2
n>2a
n.(12分)
分析:(Ⅰ)利用已知条件可得数列{b
n}与{a
n}的递推关系

,代入2b
n2=a
n+a
n+1整理,然后利用等差中项的证明数列{b
n}为等差数列
(Ⅱ)结合(1)求出数列{b
n}的公差d,进一步求得b
n,然后利用递推公式a
n=b
n-1.b
n求出a
n,通过n的特殊值猜想2
n与2a
n之间的大小关系,利用数学归纳法进行证明
点评:(1)利用递推公式进行构造,等差中项证明数列为等差数列:2a
n=a
n-1+a
n+1?数列{a
n}为等差数列
(2)利用数学归纳法证明数学命题或不等式时,要注意由归纳假设n=k成立推到n=k+1是数学归纳法的关键.

 ,比较2n与2an的大小.
,比较2n与2an的大小.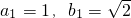 及式①、②易得
及式①、②易得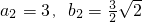 ,
, ,
, ,(5分)
,(5分)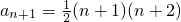 ,
, ,③
,③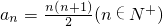 .(6分)
.(6分) ,代入2bn2=an+an+1整理,然后利用等差中项的证明数列{bn}为等差数列
,代入2bn2=an+an+1整理,然后利用等差中项的证明数列{bn}为等差数列
