
【题目】如图是某算法的程序框图,若程序运行后输出的结果是14,则判断框内填入的条件可以是( ) 
A.S≥10?
B.S≥14?
C.n>4?
D.n>5?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,某机械厂要将长![]() ,宽
,宽![]() 的长方形铁皮
的长方形铁皮![]() 进行裁剪.已知点
进行裁剪.已知点![]() 为
为![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,裁剪时先将四边形
上,裁剪时先将四边形![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 处(点
处(点![]() 分别落在直线
分别落在直线![]() 下方点
下方点![]() 处,
处,![]() 交边
交边![]() 于点
于点![]() ),再沿直线
),再沿直线![]() 裁剪.
裁剪.

(1)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并求其面积;
的形状,并求其面积;
(2)若使裁剪得到的四边形![]() 面积最大,请给出裁剪方案,并说明理由.
面积最大,请给出裁剪方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AB∥CD,AD⊥AB,AB=2CD=4,AD=2,过点C作CO⊥AB,垂足为O,将△OBC沿CO折起,如图2使得平面CBO与平面AOCD所成的二面角的大小为θ(0<θ<π),E,F分别为BC,AO的中点 
(1)求证:EF∥平面ABD
(2)若θ= ![]() ,求二面角F﹣BD﹣O的余弦值.
,求二面角F﹣BD﹣O的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 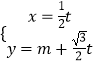 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(1)若直线l与曲线C没有公共点,求m的取值范围;
(2)若m=0,求直线l被曲线C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C的顶点在原点O,过点![]() ,其焦点F在x轴上.
,其焦点F在x轴上.
![]() 求抛物线C的标准方程;
求抛物线C的标准方程;
![]() 斜率为1且与点F的距离为
斜率为1且与点F的距离为![]() 的直线
的直线![]() 与x轴交于点M,且点M的横坐标大于1,求点M的坐标;
与x轴交于点M,且点M的横坐标大于1,求点M的坐标;
![]() 是否存在过点M的直线l,使l与C交于P、Q两点,且
是否存在过点M的直线l,使l与C交于P、Q两点,且![]() 若存在,求出直线l的方程;若不存在,说明理由.
若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2是双曲线C1: ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点,且F2是抛物线C2:y2=2px(p>0)的焦点,P是双曲线C1与抛物线C2在第一象限内的交点,线段PF2的中点为M,且|OM|=
=1(a>0,b>0)的左、右焦点,且F2是抛物线C2:y2=2px(p>0)的焦点,P是双曲线C1与抛物线C2在第一象限内的交点,线段PF2的中点为M,且|OM|= ![]() |F1F2|,其中O为坐标原点,则双曲线C1的离心率是( )
|F1F2|,其中O为坐标原点,则双曲线C1的离心率是( )
A.2+ ![]()
B.1+ ![]()
C.2+ ![]()
D.1+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com