练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

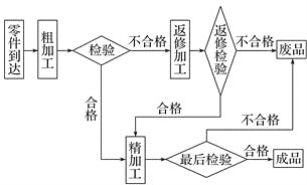
    【题目】按照图中的工序流程，从零件到成品最少要经过_______道加工和检验程序，导致废品的产生有______种不同的情形

    【答案】 4. 3.

    【解析】分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知这是一个零件的加工工序图，逐步分析该工序流程图，不难得到加工和检验程序及导致废品的产生有多少种不同的工序数目.

    详解：由流程图可知，该零件加工过程中，最少要经历：

    ①零件到达②粗加工③检验④精加工⑤最后检验.

    从零件到成品最少要经过4道加工和检验程序，

    由流程图可知，该零件加工过程中，导致废品的产生有下列几种不同的情形：

    ①零件到达粗加工检验返修加工返修检验废品，

    ②零件到达粗加工检验精加工返修检验废品，

    ③零件到达粗加工检验返修加工最后检验废品，

    共3种情形.

    故答案为：4，3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设P1 ， P2 ， …Pn为平面α内的n个点，在平面α内的所有点中，若点P到点P1 ， P2 ， …Pn的距离之和最小，则称点P为P1 ， P2 ， …Pn的一个“中位点”，例如，线段AB上的任意点都是端点A，B的中位点，现有下列命题：
    ①若三个点A、B、C共线，C在线段AB上，则C是A，B，C的中位点；
    ②直角三角形斜边的中点是该直角三角形三个顶点的中位点；
    ③若四个点A、B、C、D共线，则它们的中位点存在且唯一；
    ④梯形对角线的交点是该梯形四个顶点的唯一中位点．
    其中的真命题是（写出所有真命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （Ⅰ）当时，解不等式：；

    （Ⅱ）当时，存在最小值，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某校有一块形如直角三角形ABC的空地，其中∠B为直角，AB长40米，BC长50米，现欲在此空地上建造一间健身房，其占地形状为矩形，且B为矩形的一个顶点，求该健身房的最大占地面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设全集为R，函数 的定义域为M，则RM为（ ）
    A.[﹣1，1]
    B.（﹣1，1）
    C.（﹣∞，﹣1]∪[1，+∞）
    D.（﹣∞，﹣1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中错误的是（ ）

    A. 若两个平面平行，则分别位于这两个平面的直线也互相平行

    B. 平行于同一个平面的两个平面平行；

    C. 平面内一个三角形各边所在的直线都与另一个平面平行，则这两个平面平行

    D. 若两个平面平行，则其中一个平面内的直线平行于另一个平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设{an}是公比为q的等比数列．
    （1）试推导{an}的前n项和公式；
    （2）设q≠1，证明数列{an+1}不是等比数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中.

    （1）讨论函数极值点的个数，并说明理由；

    （2）若，成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点O（0，0），A（0，b），B（a，a3），若△OAB为直角三角形，则必有（ ）
    A.b=a3
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案