
【题目】把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点. 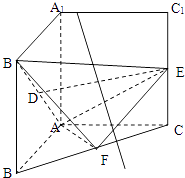
(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求二面角A﹣EB1﹣F的大小.
【答案】
(1)解:设AB的中点为G,连接DG,CG
∵D是A1B的中点
∴DG∥A1A且DG= ![]()
∵E是C1C的中点
∴CE∥A1A且CE= ![]() ,
,
∴CE∥DG且CE=DG
∴CEDG是平行四边形,
∴DE∥GC
∵DE平面ABC,GC平面ABC,
∴DE∥平面ABC
(2)解:∵△ABC为等腰直角三角形,∠BAC=90°,且F是BC的中点
∴AF⊥BC
∵平面ABC⊥平面BCC1B1
∴AF⊥平面BCC1B1
∴AF⊥B1F
设AB=AA1=2,则在B1FE中, ![]() ,
,
则 ![]() ,B1E=3
,B1E=3
∴ ![]()
∴△B1FE是直角三角形,
∴B1F⊥EF
∵AF∩EF=F
∴B1F⊥平面AEF
(3)解:分别以AB,AC,AA1为x,y,z轴建立空间直角
坐标系A﹣xyz如图,
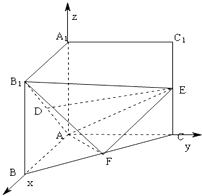
设AB=AA1=2,则
设A(0,0,0),B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1)
∵AF⊥平面BCC1B1,
∴面B1FE的法向量为 ![]() =(1,1,0),
=(1,1,0),
设平面AB1E的法向量为 ![]() ,
,
∵ ![]() ,
, ![]()
∴ ![]() ,
, ![]() ,
,
∴2y+z=0,,x+z=0,
不妨设z=﹣2,可得 ![]()
∴ 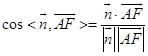 =
= ![]()
∵二面角A﹣EB1﹣F是锐角,
∴二面角A﹣EB1﹣F的大小45°
【解析】(1)取AB的中点为G,连接DG,CG;根据条件可以得到CEDG是平行四边形即可得到结论;(2)直接把问题转化为证明AF⊥B1F以及B1F⊥EF;(3)先建立空间直角坐标系,求出两个半平面的法向量,再代入向量的夹角计算公式即可.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=2,AD=4,PA⊥底面ABCD,PD与底面ABCD成30°角,E是PD的中点. 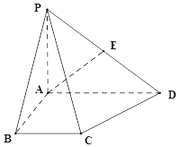
(1)点H在AC上且EH⊥AC,求 ![]() 的坐标;
的坐标;
(2)求AE与平面PCD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() ,其中,
,其中, ![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() 有
有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若数列![]() 满足
满足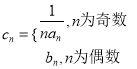 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2![]() .
.
(1)求角A的大小;
(2)若D为BC的中点,求线段AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲船以每小时15 ![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里,当甲船航行40分钟到达A2处时,乙船航行到甲船的南偏西45°方向的B2处,此时两船相距10海里,问乙船每小时航行多少海里?
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里,当甲船航行40分钟到达A2处时,乙船航行到甲船的南偏西45°方向的B2处,此时两船相距10海里,问乙船每小时航行多少海里? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com