
【题目】已知函数f(x)=ex﹣ax﹣1,(a为实数),g(x)=lnx﹣x
(1)讨论函数f(x)的单调区间;
(2)求函数g(x)的极值;
(3)求证:lnx<x<ex(x>0)
【答案】
(1)解:由题意得f′(x)=ex﹣a
当a≤0时,f′(x)>0恒成立,函数f(x)在R上单调递增,
当a>0时,由f′(x)>0可得x>lna,由f′(x)<0可得x<lna,
故函数f(x)在(lna,+∞)上单调递增,在(﹣∞,lna)上单调递减
(2)解:函数g(x)的定义域为(0,+∞), ![]() ,
,
由g′(x)>0可得0<x<1;由g′(x)<0,可得x>1.
所以函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故函数g(x)在x=1取得极大值,其极大值为ln1﹣1=﹣1
(3)证明:当a=1时,f(x)=ex﹣x﹣1,
由(1)知,f(x)=ex﹣x﹣1在x=ln1=0处取得极小值,也是最小值,
且f(x)min=0,故ex﹣x﹣1>0(x>0),得到ex>x+1(x>0).
由(2)知,g(x)=lnx﹣x在x=l处取得最大值,且g(x)max=﹣1,
故lnx﹣x≤﹣1(x>0),得到lnx≤x﹣1<x(x>0).
综上lnx<x<ex(x>0).
【解析】(1)求导数得到f′(x)=ex﹣a,然后讨论a的符号,从而可判断导数符号,这样即可求出每种情况下函数f(x)的单调区间;(2)可先求出函数g(x)的定义域,然后求导,判断导数的符号,从而根据极值的概念求出函数g(x)的极值;(3)可知a=1时,f(x)在x=0处取得极小值,从而可得出ex>x+1,而由(2)可知g(x)在x=1处取得极大值,也是最大值﹣1,这样即可得出lnx≤x﹣1<x,这样便可得出要证的结论.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的图象经过点(0,﹣1).
)的图象经过点(0,﹣1).
(1)求函数f(x)的对称轴方程及相邻两条对称轴间的距离d;
(2)设α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.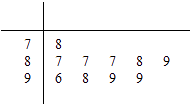
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为 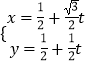 (t为参数),点A的极坐标为(
(t为参数),点A的极坐标为( ![]() ,
, ![]() ),设直线l与圆C交于点P、Q.
),设直线l与圆C交于点P、Q.
(1)写出圆C的直角坐标方程;
(2)求|AP||AQ|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com