
【题目】电脑每秒钟以相同的概率输出一个数字1或2.将输出的前![]() 个数字之和被3整除的概率记为
个数字之和被3整除的概率记为![]() .证明:
.证明:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)见解析(2)见解析
【解析】
证法1 这![]() 个数字共有
个数字共有![]() 种可能情形.
种可能情形.
设其中数字和被3整除的有![]() 种.则不被3整除的有
种.则不被3整除的有![]() 种.
种.
对于![]() 个数字的情形,若其和被3整除,则前
个数字的情形,若其和被3整除,则前![]() 个数字之和不被3整除;反之,对于前
个数字之和不被3整除;反之,对于前![]() 各数字之和不被3整除的每种情形,有唯一的第
各数字之和不被3整除的每种情形,有唯一的第![]() 个数字可使前
个数字可使前![]() 个数字之和被3整除.因此,
个数字之和被3整除.因此,![]() .
.
这表明,概率![]() 满足递推关系式
满足递推关系式![]()
![]()
![]()
![]() .
.
证法2 若输出的前![]() 个数字之和被3整除的概率为
个数字之和被3整除的概率为![]() ,则不被3整除的概率为
,则不被3整除的概率为![]() .要使输出的前
.要使输出的前![]() 个数字之和被3整除,则必须使前
个数字之和被3整除,则必须使前![]() 个数字之和不被3整除,且此时第
个数字之和不被3整除,且此时第![]() 个数字也随之确定.
个数字也随之确定.
所以,由条件概率的公式得![]() .
.
余下同证法1.
证法3 ![]() 个数字共有
个数字共有![]() 种可能情形.
种可能情形.
下面计算其和被3整除的种数,这等于多项式![]() 的展开式中
的展开式中![]() 等项的系数之和,即
等项的系数之和,即![]() ,①
,①
其中,![]() 为三次单位根,
为三次单位根,![]() 是其共轭复数.
是其共轭复数.
故式①![]() .
.
因此,所求的概率为![]() .
.
可验证![]() 及
及![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别是240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动。
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作,求事件M“抽取的2名同学来自同一年级”发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线方程为![]() .
.
(1)证明:直线恒过定点;
(2)![]() 为何值时,点
为何值时,点![]() 到直线的距离最大,最大值为多少?
到直线的距离最大,最大值为多少?
(3)若直线分别与![]() 轴,
轴,![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,求
两点,求![]() 面积的最小值及此时直线的方程.
面积的最小值及此时直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在原点,半径为
的圆心在原点,半径为![]() ,若圆
,若圆![]() 与坐标轴的交点为顶点的四边形是一个面积为
与坐标轴的交点为顶点的四边形是一个面积为![]() 的正方形(记为
的正方形(记为![]() )设点
)设点![]() 在
在![]() 轴的负半轴上,以点
轴的负半轴上,以点![]() 、
、![]() 和点
和点![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() .
.
(1)求圆![]() 的半径
的半径![]() 及点
及点![]() 的坐标;
的坐标;
(2)若过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,当线段
两点,当线段![]() 的中点落在正方形
的中点落在正方形![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,某公交公司分别推出支付宝和徽信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表l所示:
表1

根据以上数据,绘制了如右图所示的散点图.
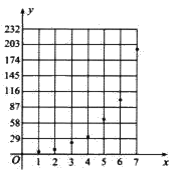
(1)根据散点图判断,在推广期内,![]() (c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次;
参考数据:

其中![]()
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: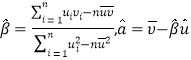 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)将曲线![]() 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线![]() ,若
,若![]() ,
, ![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com