
����Ŀ�����й�ʣ�ඨ�����ֳ������Ӷ�������1852�꣬Ӣ����������ʿΰ���������������㾭�������ﲻ֪��������Ľⷨ����ŷ�ޣ�1874�꣬Ӣ����ѧ������ɭָ���˷�����1801���ɸ�˹�õ��Ĺ���ͬ��ʽ�ⷨ��һ���Զ��������������֮Ϊ���й�ʣ�ඨ���������й�ʣ�ඨ����������һ���������������⣬��������һ���������⣺��1��2019��2019�����У��ܱ�3����2�ұ�5������2��������С�����˳���ų�һ�У���������![]() ����������������У��м����ֵΪ��������
����������������У��м����ֵΪ��������
A.992B.1022C.1007D.1037
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �Ǿ��Σ��ضԽ���
�Ǿ��Σ��ضԽ���![]() ��
��![]() ����ʹ�õ�
����ʹ�õ�![]() ��ƽ��
��ƽ��![]() �ϵ���Ӱǡ�����ڱ�
�ϵ���Ӱǡ�����ڱ�![]() ��.
��.
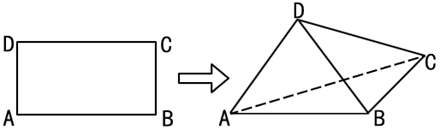
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ʱ��������
ʱ��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014�꣬�������Ժ�칫��ӡ������������ũ�����ؾ�ӪȨ������ת��չũҵ�ʶȹ�ģ��Ӫ���������Ҫ�������չ������ת���ʶȹ�ģ��Ӫ.ij������2015�꿪ʼ�а���һ�����Ĵ��ģˮ����ֲˮ����������һ��ˮ���ո������̨������ˮ���ո������ʹ���������ӣ�ÿ���������Ҳ��Ӧ���ӣ�����ˮ���ո���Թ���ʹ��֮����5������ƽ��ÿ̨ˮ���ո����������������ͳ�����£�
��� | 2015 | 2016 | 2017 | 2018 | 2019 |
��ݴ��� | 1 | 2 | 3 | 4 | 5 |
�������� | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
��1������5���������ȡ2�꣬��ƽ��ÿ̨ˮ���ո��ÿ�����������������1�����2��Ԫ�ĸ��ʣ�
��2����![]() ����
����![]() �����Իع鷽�̣�
�����Իع鷽�̣�
��3������ˮ���ո���Ĺ���۸���ÿ̨16��Ԫ����(2)�еĻع鷽�̣���ÿ̨ˮ���ո������ƽ�����ýǶȣ�����Ϊһ̨��ˮ���ո����ʹ����5�����̭�����Ǽ���ʹ�õ���8������̭��
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��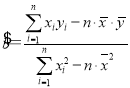 ��
��![]()
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������彡��״����ֱ�ӷ�Ӧ��һ����Ϊ������Ҹ���¶�![]() ����λ��
����λ��![]() ��ƽ����
��ƽ����![]() ֮�伴Ϊ�������£�����
֮�伴Ϊ�������£�����![]() ��Ϊ����.����״̬�£���ͬ���¿ɷֳ��������ַ������ͣ����ȣ�
��Ϊ����.����״̬�£���ͬ���¿ɷֳ��������ַ������ͣ����ȣ�![]() �����ȣ�
�����ȣ�![]() �������ȣ�������Σ�գ���
�������ȣ�������Σ�գ���![]() .
.
ijλ���������ȣ���12����26��סԺ����. ҽ�����ݲ���仯����14�տ�ʼ����3��Ϊһ���Ƴ̣��ֱ������ֲ�ͬ�Ŀ�����Ϊ�û��߽�����������. סԺ�ڼ䣬����ÿ������8:00��ҩ����ʿÿ������16:00Ϊ���߲���Ҹ�����¼�¼���£�

��1���������סԺ�ڼ�û������²�����![]() �ĸ�������ƽ��ֵ��
�ĸ�������ƽ��ֵ��
��2����![]() ����
����![]() ���ڼ䣬ҽ�������ѡȡ
���ڼ䣬ҽ�������ѡȡ![]() ���ڲ������µ�ͬʱΪ�û��߽���ijһ������Ŀ��
���ڲ������µ�ͬʱΪ�û��߽���ijһ������Ŀ��![]() ��Ŀ���ļ�飬��
��Ŀ���ļ�飬��![]() Ϊ��������������
Ϊ��������������![]() ��Ŀ����������������
��Ŀ����������������![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
��3������������һ���ڷ�ҩ��2-8��Сʱ���ܳ���ѪҺŨ�ȵĸ߷壬��ʼɱ��ϸ�����ﵽ��������Ч��.�������ֿ���������Ч��������������ݱ������ݣ��ж����ֿ���������Ч����ѣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() ������
������![]() ������
������![]() ���Ͻصõ��ҳ�
���Ͻصõ��ҳ�![]() ���趯ԲԲ��
���趯ԲԲ��![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ��
��
��1��������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ�߽�����
��ֱ�߽�����![]() ��
��![]() ���㣬��������
���㣬��������![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ�õ�
��ʹ�õ�![]() ����
����![]() Ϊֱ����Բ�ϣ������ڣ������
Ϊֱ����Բ�ϣ������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������÷ɭ��17���ͷ�����������ѧ�Һ���ʿ��Ҳ�ǵ�ʱŷ��ѧ��һλ���ص��������÷ɭ��ŷ����á����������о��Ļ����϶�2p��1���˴����ļ��㡢��֤����������Ϊ�˼���÷ɭ�����۷������һ���ף�������2P��1������p������������������Ϊ÷ɭ����.��ִ����ͼ��ʾ�ij����ͼ���������÷ɭ�����ĸ����ǣ� ��
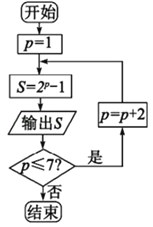
A.3B.4C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊֱ�����Σ�
Ϊֱ�����Σ�![]() ��
��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() ��
��![]() .
.
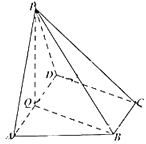
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������ֱ��![]() ��
��![]() ���ɽ�Ϊ
���ɽ�Ϊ![]() ����
����![]() �ij���
�ij���
��3���ڣ�2���������£���ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ.
���������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ΪԲ
ΪԲ![]() ��
��![]() ��һ���㣬����
��һ���㣬����![]() �ֱ���
�ֱ���![]() �ᣬ
�ᣬ![]() ��Ĵ��ߣ�����ֱ�Ϊ
��Ĵ��ߣ�����ֱ�Ϊ![]() ��
��![]() ������
������![]() �ӳ�����
�ӳ�����![]() ��ʹ��
��ʹ��![]() ����
����![]() �Ĺ켣��Ϊ����
�Ĺ켣��Ϊ����![]() .
.
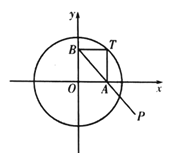
��1��������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��
��![]() �ֱ�λ��
�ֱ�λ��![]() ����
����![]() ����������ϣ�ֱ��
����������ϣ�ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ������������
������������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ���ı���
��ʹ���ı���![]() Ϊƽ���ı��Σ������ڣ����ֱ��
Ϊƽ���ı��Σ������ڣ����ֱ��![]() ���̣��������ڣ�˵������.
���̣��������ڣ�˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com