(1)证明:由题意,x
1≤x≤x
2,∴x
1≤λx
1+(1-λ)x
2≤x
2,∴x
1-x
2≤λ(x
1-x
2)≤0.
∵x
1-x
2<0,∴0≤λ≤1;
(2)解:∵

=λ

+(1-λ)

,∴

,∴
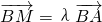
∴B、M、A三点在一条直线上.
又由(1)的结论,M在线段AB上,且与点P的横坐标相同.
对于[0,1]上的函数y=x
2,A(0,0),B(1,1),
则有P(x,x
2),M(x,x),∴

=x-x
2∈[0,

];
同理对于[0,1]上的函数y=x
3,

=x-x
3,
令g(x)=x-x
3,则g′(x)=1-3x
2,
∵x∈(0,

)时,g′(x)>0;x∈(

,1)时,g′(x)<0
∴g(x)在(0,

)上单调递增;在(

,1)上单调递减
∴g(x)在x=

处取得最大值
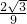
,而g(0)=g(1)=0,∴

∈[0,
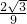
]
∵
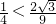
∴k∈
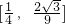
时,函数y=x
2与y=x
3中有且只有一个可在标准k下线性近似.
分析:(1)据区间的左端点小于等于右端点,列出x
1≤x≤x
2,将x的值代入解不等式,即可证得结论;
(2)对于y=x
2与y=x
3分别求出M,P两点的距离的最大值,利用题目中的定义求出k的范围即可.
点评:本题考查新定义,考查函数的最值,考查学生的计算能力,考查向量知识的运用,属于中档题.

 =(x1,y1),
=(x1,y1), =(x2,y2),且x=λx1+(1-λ)x2;记
=(x2,y2),且x=λx1+(1-λ)x2;记 =λ
=λ +(1-λ)
+(1-λ) ,现定义“当
,现定义“当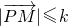 (k为正的常数)恒成立时,称函数y=f (x)在[x1,x2]上可在标准k下线性近似”.
(k为正的常数)恒成立时,称函数y=f (x)在[x1,x2]上可在标准k下线性近似”. =λ
=λ +(1-λ)
+(1-λ) ,∴
,∴ ,∴
,∴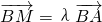
 =x-x2∈[0,
=x-x2∈[0, ];
]; =x-x3,
=x-x3, )时,g′(x)>0;x∈(
)时,g′(x)>0;x∈( ,1)时,g′(x)<0
,1)时,g′(x)<0 )上单调递增;在(
)上单调递增;在( ,1)上单调递减
,1)上单调递减 处取得最大值
处取得最大值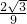 ,而g(0)=g(1)=0,∴
,而g(0)=g(1)=0,∴ ∈[0,
∈[0,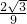 ]
]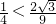
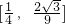 时,函数y=x2与y=x3中有且只有一个可在标准k下线性近似.
时,函数y=x2与y=x3中有且只有一个可在标准k下线性近似.

![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),
=(x2,y2),![]() =(x,y),若x=λx1+(1-λ)x2,记向量
=(x,y),若x=λx1+(1-λ)x2,记向量![]() =λ
=λ![]() +(1-λ)
+(1-λ)![]() .现在定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指
.现在定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指![]() ≤k恒成立,其中k是一个人为确定的正数.
≤k恒成立,其中k是一个人为确定的正数.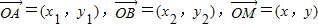 ,若x=λx1+(1-λ)x2,记向量
,若x=λx1+(1-λ)x2,记向量 ,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指
,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指 恒成立,其中K是一个正数.
恒成立,其中K是一个正数.