
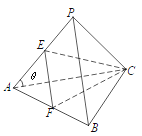
【题目】已知三棱锥![]() 的四个顶点在球
的四个顶点在球![]() 的球面上,
的球面上,![]() ,
,![]() 是边长为
是边长为![]() 正三角形,
正三角形,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,则球
,则球![]() 的体积为_________________。
的体积为_________________。
【答案】![]()
【解析】
由已知设出![]() ,
,![]() ,
,![]() ,分别在
,分别在![]() 中和在
中和在![]() 中运用余弦定理表示
中运用余弦定理表示![]() ,得到关于x与y的关系式,再在
,得到关于x与y的关系式,再在![]() 中运用勾股定理得到关于x与y的又一关系式,联立可解得x,y,从而分析出正三棱锥是
中运用勾股定理得到关于x与y的又一关系式,联立可解得x,y,从而分析出正三棱锥是![]() ,
,![]() ,
,![]() 两两垂直的正三棱锥,所以三棱锥
两两垂直的正三棱锥,所以三棱锥![]() 的外接球就是以
的外接球就是以![]() 为棱的正方体的外接球,再通过正方体的外接球的直径等于正方体的体对角线的长求出球的半径,再求出球的体积.
为棱的正方体的外接球,再通过正方体的外接球的直径等于正方体的体对角线的长求出球的半径,再求出球的体积.
在![]() 中,设
中,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为点![]() ,点
,点![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,
,
整理得![]() ,
,
因为![]() 是边长为
是边长为![]() 的正三角形,所以
的正三角形,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,由
,由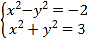 ,解得
,解得![]() ,
,
所以![]() 。
。
又因为![]() 是边长为
是边长为![]() 的正三角形,所以
的正三角形,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
则球![]() 为以
为以![]() 为棱的正方体的外接球,
为棱的正方体的外接球,
则外接球直径为![]() ,
,
所以球![]() 的体积为
的体积为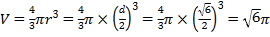 ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在一次数学测验后,数学老师将某班全体学生(50人)的数学成绩进行初步统计后交给其班主任(如表).
分数 | 5060 | 60~70 | 70-80 | 80-90 | 90~100 |
人数 | 2 | 6 | 10 | 20 | 12 |
请你帮助这位班主任完成下面的统计分析工作:
(1)列出频率分布表;
(2)画出频率分布直方图及频率折线图;
(3)从频率分布直方图估计出该班同学成绩的众数、中位数和平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与
与![]() 的交点的轨迹
的交点的轨迹![]() 的方程;
的方程;
(2)若曲线![]() 上存在4个点到直线
上存在4个点到直线![]() 的距离相等,求实数
的距离相等,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务.已知:①食物投掷地点有远、近两处;②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处,那么不同的搜寻方案有______种.(以数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为 为参数
为参数![]() .
.
![]() 若
若![]() ,直线l与x轴的交点为M,N是圆C上一动点,求
,直线l与x轴的交点为M,N是圆C上一动点,求![]() 的最小值;
的最小值;
![]() 若直线l被圆C截得的弦长等于圆C的半径,求a的值.
若直线l被圆C截得的弦长等于圆C的半径,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,研究小组在实验室对该种微生物进行培育实验.前三天观测的该微生物的群落单位数量分别为12,16,24.根据实验数据,用y表示第![]() 天的群落单位数量,某研究员提出了两种函数模型;①
天的群落单位数量,某研究员提出了两种函数模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常数.
,其中a,b,c,p,q,r都是常数.
(1)根据实验数据,分别求出这两种函数模型的解析式;
(2)若第4天和第5天观测的群落单位数量分别为40和72,请从这两个函数模型中选出更合适的一个,并计算从第几天开始该微生物群落的单位数量超过1000.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行硏究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差x( | 8 | 11 | 13 | 12 | 10 |
发芽数y(颗) | 22 | 27 | 31 | 35 | 26 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均不小于27”的概率.
(2)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程![]() .
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(参考公式:回归直线的方程是![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com