
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,点
,点![]() 为短轴的一个端点,
为短轴的一个端点,![]() .
.
(1)求椭圆C的方程;
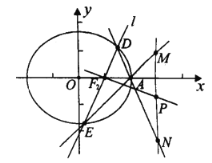
(2)如图,过右焦点![]() ,且斜率为k(
,且斜率为k(![]() )的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线
)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点M,N,线段
于点M,N,线段![]() 的中点为P,记直线
的中点为P,记直线![]() 的斜率为
的斜率为![]() .试问
.试问![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
科目:高中数学 来源: 题型:
【题目】2021年起,新高考科目设置采用“![]() ”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
①样本中的女生更倾向于选历史;
②样本中的男生更倾向于选物理;
③样本中的男生和女生数量一样多;
④样本中意向物理的学生数量多于意向历史的学生数量.
根据两幅条形图的信息,可以判断上述结论正确的有( )


A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物.虽然
微米的颗粒物,也称为可入肺颗粒物.虽然![]() 只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.我国
只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.我国![]() 标准如下表所示.我市环保局从市区四个监测点2018年全年每天的
标准如下表所示.我市环保局从市区四个监测点2018年全年每天的![]() 监测数据中随机抽取
监测数据中随机抽取![]() 天的数据作为样本,监测值如茎叶图如图所示.
天的数据作为样本,监测值如茎叶图如图所示.
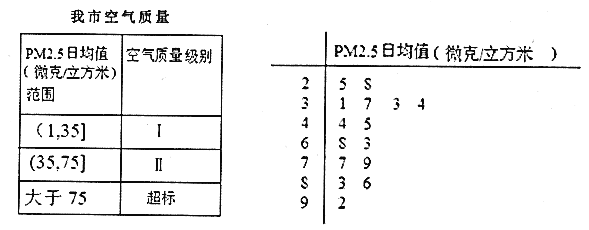
(Ⅰ)求这![]() 天数据的平均值;
天数据的平均值;
(Ⅱ)从这![]() 天的数据中任取
天的数据中任取![]() 天的数据,记表示其中空气质量达到一级的天数
天的数据,记表示其中空气质量达到一级的天数![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)以![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中大约有多少天的空气质量达到一级.
天计算)中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“四”“校”“联”“考”四个字,有放回地从中任取一个小球,取到“联”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“四”“校”“联”“考”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:13 24 12 32 43 14 24 32 31 21 23 13 32 21 24 42 13 32 23 34据此估计,直到第二次就停止的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() 处取得极值,判断当
处取得极值,判断当![]() 时,存在几条切线与直线
时,存在几条切线与直线![]() 平行,请说明理由;
平行,请说明理由;
(3)若![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
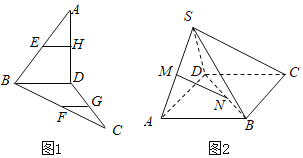
【题目】(1)如图(1)已知E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH![]() FG.求证:EH
FG.求证:EH![]() BD.
BD.
(2)如图(2):S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且![]() ,求证:MN
,求证:MN![]() 平面SBC.
平面SBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、![]() 后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
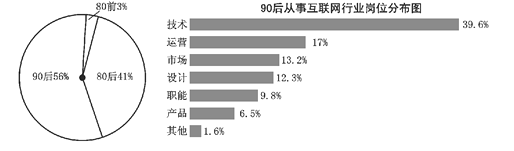
A. 互联网行业从业人员中![]() 后占一半以上
后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 前多
前多
D. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 后多
后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6 人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,
,![]() ,乙校教师记为
,乙校教师记为![]() ,
,![]() ,丙校教师记为C,丁校教师记为D.现从这6 名教师代表中选出 3 名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
,丙校教师记为C,丁校教师记为D.现从这6 名教师代表中选出 3 名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com