
【题目】在![]() 中,已知A,a,b,给出下列说法:
中,已知A,a,b,给出下列说法:
①若![]() ,则此三角形最多有一解;
,则此三角形最多有一解;
②若![]() ,且
,且![]() ,则此三角形为直角三角形,且
,则此三角形为直角三角形,且![]() ;
;
③当![]() ,且
,且![]() 时,此三角形有两解.
时,此三角形有两解.
其中正确说法的个数为( )
A.0B.1C.2D.3
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点与短轴的一个端点恰好围成一个面积为
的两个焦点与短轴的一个端点恰好围成一个面积为![]() 的等边三角形.
的等边三角形.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() 、
、![]() ,右焦点为
,右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的动点,直线
的动点,直线![]() 与椭圆
与椭圆![]() 在点
在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 运动时,试判断以
运动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一湖中有不在同一直线的三个小岛A、B、C,前期为开发旅游资源在A、B、C三岛之间已经建有索道供游客观赏,经测量可知AB两岛之间距离为3公里,BC两岛之间距离为5公里,AC两岛之间距离为7公里,现调查后发现,游客对在同一圆周上三岛A、B、C且位于![]() (优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在
(优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在![]() 上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
查看答案和解析>>
科目:高中数学 来源: 题型:
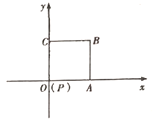
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴顺时针滚动一周,设顶点
轴顺时针滚动一周,设顶点![]() 的运动轨迹与
的运动轨迹与![]() 轴所围区域为
轴所围区域为![]() ,若在平面区域
,若在平面区域![]() 内任意取一点
内任意取一点![]() ,则所取的点
,则所取的点![]() 恰好落在区域
恰好落在区域![]() 内部的概率为
内部的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方形花圃被分成5份.
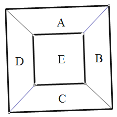
(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若将6个不同的盆栽都摆放入这5个部分,且要求每个部分至少有一个盆栽,问有多少种不同的放法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com