
【题目】如图,三棱柱![]() -
-![]() 的底面是边长为2的等边三角形,
的底面是边长为2的等边三角形,![]() 底面
底面![]() ,点
,点![]() 分别是棱
分别是棱![]() ,
,![]() 上的点,且
上的点,且![]()
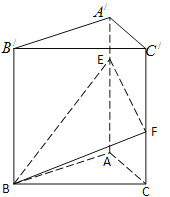
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(II)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明过程见解析;(Ⅱ)![]() .
.
【解析】试题(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,进而证的
,进而证的![]() 平面
平面![]() ,在取
,在取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,从而证得
,从而证得![]() 平面
平面![]() ,进而证的结论;
,进而证的结论;
(2)以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,求得向量
轴建立如图所示的空间直角坐标系,求得向量![]() 和平面
和平面![]() 的法向量,即可利用向量的运算得到直线与平面所成角的正弦值。
的法向量,即可利用向量的运算得到直线与平面所成角的正弦值。
试题解析:
(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
因为![]() 底面
底面![]() ,所以侧面
,所以侧面![]() 底面
底面![]() ,
,
所以![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,所以
,所以![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
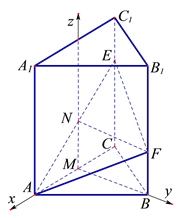
(Ⅱ)以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,因为
轴建立如图所示的空间直角坐标系,因为![]() ,依题意得
,依题意得![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由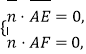 得
得![]() 令
令![]() ,得
,得![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】自新型冠状病毒疫情爆发以来,人们时刻关注疫情,特别是治愈率,治愈率![]() 累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第
累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第![]() 天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
![]() :第
:第![]() 天新增确诊人数;
天新增确诊人数;![]() :第
:第![]() 天新增治愈人数;
天新增治愈人数;![]() :第
:第![]() 天治愈率
天治愈率
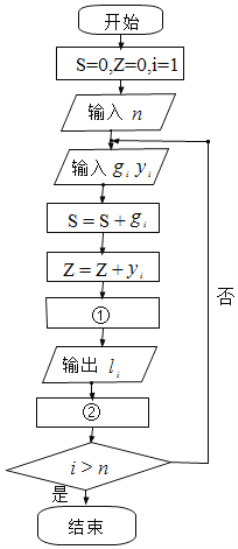
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE.求直线BC与平面ABF所成角的大小,并求线段PH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
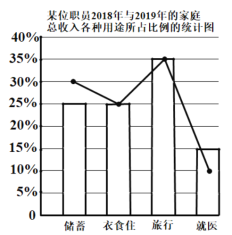
【题目】如图所示,折线图和条形图分别为某位职员2018年与2019年的家庭总收入各种用途所占比例的统计图,已知2018年的家庭总收入为10万元,2019年的储蓄总量比2018年的储蓄总量减少了10%,则下列说法:
①2019年家庭总收入比2018年增长了8%;
②年衣食住的总费用与2018年衣食住的总费相同;
③2019年的旅行总费用比2018年增加了2800元;
④2019年的就医总费用比2018年增长了5%
其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据国家统计局发布的数据,2019年11月全国CPI(居民消费价格指数),同比上涨4.5%,CPI上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响CPI上涨3.27个百分点.下图是2019年11月CPI一篮子商品权重,根据该图,下列结论错误的是( )
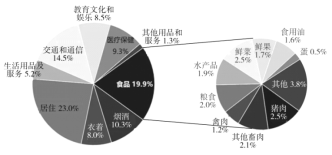
A.CPI一篮子商品中所占权重最大的是居住
B.CPI一篮子商品中吃穿住所占权重超过50%
C.猪肉在CPI一篮子商品中所占权重约为2.5%
D.猪肉与其他畜肉在CPI一篮子商品中所占权重约为0.18%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
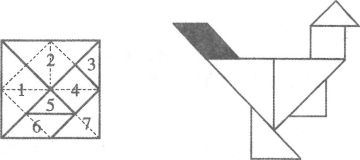
【题目】七巧板是一种古老的中国传统智力玩具,是由七块板组成的.而这七块板可拼成许多图形,例如:三角形、不规则多边形、各种人物、动物、建筑物等,清陆以湉《冷庐杂识》写道:近又有七巧图,其式五,其数七,其变化之式多至千余.在18世纪,七巧板流传到了国外,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.若用七巧板拼成一只雄鸡,在雄鸡平面图形上随机取一点,则恰好取自雄鸡鸡尾(阴影部分)的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com